Seminar stochastic geometry and its applications
Seminar Supervisor
Prof. Dr. Evgeny Spodarev
Seminar Advisor
Dr. Vitalii Makogin
Date and Place
It will be a one-day block-seminar. It takes place on 26th of January 2018, at 09:00-17:00 in room O28 - 2004.
Prerequisites
The level of difficulty in this seminar is varying between the different topics. The audience is at least supposed to be familiar with basic probability. There are a few talks that require the lecture Stochastics II.
Intended Audience
Bachelor and Master Students of any mathematical study course.
The "(B)" in the list of talks, means that this talk is supposed to be given by a Bachelor's Student.
Content
Change point analysis for random processes and fields: A change-point problem for a finite sequence of random variables X1, X2,..., XT can be formulated as follows. The sequence is said to have a change point at s if Xk, k = 1, ... , s-1 have a common distribution function F1(x); Xk , k = s + 1, ..., T have a common distribution function F2(x), and F1(x) ≠ F2(x). One considers the problem of testing the null hypothesis of ”no-change”, H0 : s = T, against the alternative of ”change”, H1 : 1 < s < T, using a non-parametric statistic.
Random sequences: Change point detection has various applications in quality control of production, search for structural breaks in econometrics and finance, spam filtering, speech recognition, medical diagnostics and so on. Methods: CUSUM procedure (cumulative sum control chart), scan statistics, Bayesian approach as well as maximum likelihood estimation are often used.
Random processes: A change point of a stochastic process is a moment of time when some probabilistic characteristics of this process change.
Random fields: For random fields, the change-point problem is a detection of a region in the index set where some probabilistic properties of this field differ from its remaining part. The involved methods include M-estimation, minimax methods for risks, geometric tube method, some nonparametric and Bayesian techniques.
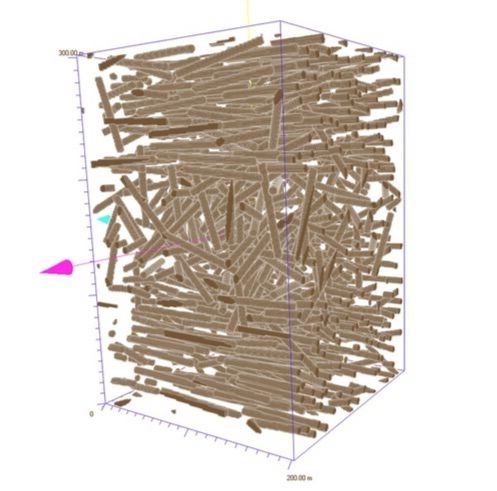
Glas fibre reinforced polymers: Change-point detection problems for geometric random fields appear e.g. in modelling of glas fibre reinforced polymers. During this process, deviations from the requested direction may occur, creating undesirable fibre clusters and/or deformations. This kind of inhomogeneities are characterized by abrupt changes in the direction of the fibres, and their detection is subject of study in the change-point analysis.
Registration
To register for the seminar, please write an E-Mail to Vitalii Makogin until 30th September 2017 (extended to 14th of October). In the e-mail please give your name, matriculation number, your course of studies and subjects you have taken in the area of Probability or Statistics.
Criteria to pass the seminar
Each student is supposed to give a talk, make slides and written presentation and to attend the seminar on a regular basis. Those who give a (good) talk and attend the seminar will pass the seminar.
List of Talks
The list of talks will be defined during the first meeting from the following group of themes.
- Change Detection Algorithms: Introduction, Limit checking detectors and shewhart control charts, Geometric moving average control charts, Finite moving average control charts, Filtered derivative algorithms. Properties of on-line algorithms -- Franz Eiglmeier
- Cumulative sum (CUSUM) and Bayes-type algorithms: CUSUM Algorithm as a repeated sequential probability ratio test, Offline statistical derivation, Geometrical interpretation in the Gaussian case, Unknown parameter after change, Change detection and tracking. (B)
- A posteriori methods of change-point detection. An abrupt change-point -- Ilia Khomenko.
- A posteriori methods of change-point detection. A disappearing and multible disorder -- Vitalii Makogin
- Disorder detection of random fields: Methods of detection of the parametric disorder regions. -- Dmytro Bigun.
- Disorder detection of random fields: Methods of detection of the nonparametric disorder regions, Binary problem. -- Ruslana Kuksova.
- Inhomogeneities in Glas fibre reinforced polymers: homogeneous Poisson marked point process, Kernel density estimator of the mark distribution, Entropy estimator, A CLT for entropy -- Hung Do Tien.
Literature:
- M. Basseville and I.V. Nikiforov, Detection of abrupt changes: theory and application, 1993.
- B. E. Brodsky and B. S. Darkhovsky, Nonparametric methods in change-point problems, Math. and its Appl., vol. 243, 1993.
- B. E. Brodsky and B. S. Darkhovsky, Non-parametric statistical diagnosis, Math. and its Appl., vol. 509, 2000, Problems and methods.
- Alonso-Ruiz, P., & Spodarev, E. (2017). Estimation of entropy for Poisson marked point processes. Advances in Applied Probability, 49(1), 258-278.
Contact
- Office hours: Wednesday 4 - 5 pm
- Phone: +49 (0)731/50-23530
- <link en mawi institute-of-stochastics mitarbeiter evgeny-spodarev.html _self internal-link>Homepage
Seminar Advisor
News
If you are interested in a talk then
write an e-mail to vitalii.makogin(at)uni-ulm.de
Duration of the talk: 45-60 minutes.
Talks will be held in English.
- The organizing meeting will be will be in He22, E03 at 14:00-15:00 on Friday, 27th of October.