Potentialtopf-Modelle

Welche Informationen über den Zustand der Quantenobjekte können wir aus der stationären Schrödinger-Gleichung gewinnen?

Bevor wir die Schrödinger-Gleichung auf die Elektronen in der Atomhülle anwenden, beschäftigen wir uns mit einem einfacheren Fall. Wir stellen uns ein Elektron in einem linearen Raumbereich eingesperrt vor, z. B. in einem Geradenabschnitt der Länge L. Es sollen keine Kräfte auf das Elektron wirken, deshalb ist seine potentielle Energie in diesem Bereich gleich Null. Dabei wird sich das Elektron nur dann ausschließlich auf der Strecke 0 < x < L bewegen, wenn allen x < 0 und x > L die potentielle Energie V(x) =  zugeordnet wird. Das Elektron befindet sich also in einem linearen oder eindimensionalen Potentialtopf. Wenn ein ganzzahliges Vielfaches n der halben de-Broglie-Wellenlänge auf diese eingegrenzte Strecke passt, bilden sich wie in der klassischen Mechanik stehende Wellen:

(12.1)

Diese Wellen haben demnach nur ganz bestimmte Wellenlängen  = 2L/n  und somit auch nur folgende Impulse: p = h/ = (h/2L)  n . Daraus ergeben sich die möglichen Energiewerte des Elektrons:

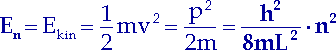
(12.2)

Die Energie eines Teilchens der Masse m im eindimensionalen Potentialtopf der Breite L mit unendlich hohen Wänden kann nur diskrete Werte annehmen. Der kleinste Energiewert ist nicht Null, da n immer eine positive ganze Zahl ist. Der tiefste Energiezustand ergibt sich für n = 1:

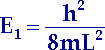
(12.3)

Deswegen kann sich ein Materieobjekt auch bei niedrigsten Temperaturen (auch bei 0 K) nie in Ruhe befinden. E ₁ wird Nullpunktenergie genannt.

Versuchen wir nun die zeitunabhängige Schrödinger-Gleichung auf ein Elektron im linearen Potentialtopf anzuwenden. Wegen V(x) = 0 vereinfacht sich diese Gleichung mit B² = 2mE/² zur folgenden Form:

(12.4)

Differentialgleichungen dieser Art kennen wir aus der Mechanik als Schwingungsgleichungen. Die zweite Ableitung der Wellenfunktion soll also bis auf den konstanten Faktor B² mit der Wellenfunktion übereinstimmen. Sowohl die Sinus- als auch die Kosinusfunktion erfüllen diese Forderung. Darüber hinaus muss die Aufenthaltswahrscheinlichkeit des Elektrons  ² in den Wänden und außerhalb des Potentialtopfes Null sein. Die Wellenfunktion ist stetig, deswegen muss auch sie dort Null sein: (0) = 0 und (L) = 0. Aufgrund der ersten Randbedingung kommt die Kosinusfunktion nicht in Frage. Unser Ansatz zur Lösung der Schrödinger-Gleichung sieht dann so aus:

(12.5)

Die zweite Randbedingung (L) = A  sin(B  L) = 0 wird erfüllt, wenn gilt: B  L = n   mit n = 1, 2, 3,... . Das liefert uns B =  = n  /L. Daraus erhalten wir die Formel (12.2), die wir oben mit der de-Broglie-Beziehung für stehende Wellen gewonnen haben.

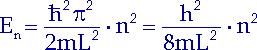
(12.6)

Außerdem können wir jetzt die Wellenfunktionen ermitteln. Im Ansatz (12.5) ist uns jetzt nur der Koeffizient A unbekannt: _n(x) = A  sin((n  /L)  x). Um A zu berechnen, verwenden wir folgende Normierungsbedingung: Die Wahrscheinlichkeit, das Elektron im gesamten Bereich von 0 bis L anzutreffen, ist 100%, also gleich 1:

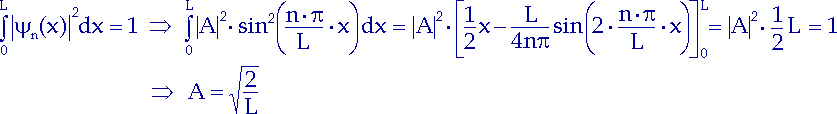
	(12.7)

Schließlich erhalten wir

Lösungen der Schrödinger-Gleichung für eindimensional gebundenes Elektron

(12.8)

Im Bild unten sehen wir stehende Wellen eines Elektrons bei unterschiedlichen Energiewerten (n = 1, 2, 3) in einem eindimensionalen Potentialtopf.  ² ist die Wahrscheinlichkeitsdichte für den Ort des Elektrons. Im Falle einer reellwertigen Wellenfunktion ist sie einfach das Quadrat dieser Funktion. Das Produkt  ²   x gibt die Wahrscheinlichkeit dafür an, dass sich das Elektron am Ort x im Abschnitt x befindet. Die Wahrscheinlichkeit, das Elektron außerhalb des definierten Raumbereichs zu finden, ist gleich Null. Deswegen muss die Wellenfunktion an den Wänden des Potentialtopfs Knotenpunkte aufweisen.

Zur Vereinfachung ist unser Potentialkasten ein undurchlässiger Würfel mit Kantenlängen L. Die Schrödinger-Gleichung lautet hier:
	(12.9)
mit Randbedingungen  = 0 für x = 0, x = L, y = 0, y = L, z = 0, z = L.

Der Lösungsansatz zu dieser Gleichung ist das Produkt von unabhängigen Sinusfunktionen, dessen Argumente analog zum Ansatz (12.5) jeweils eine Ortsvariable x, y bzw. z und ihr zugehörige Quantenzahl n_x , n_y bzw. n_z enthalten:

(12.10)

Die Quantenzahlen sind voneinander unabhängig.

Die Abbildung unten zeigt die Aufenthaltswahrscheinlichkeitsdichte  ² eines Elektrons im dreidimensionalen Potentialtopf nach unterschiedlichen Kombinationen von Quantenzahlen. Je dunkler ein Bereich im Kasten erscheint, desto größer ist dort der Wert von  ². Mit Nullstellen der - Funktion ergeben sich Knotenflächen analog zu den Knotenpunkten einer stehenden eindimensionalen Welle.

Nach Einsetzen des Lösungsansatzes (12.10) in die Schrödinger-Gleichung (12.9) erhalten wir gequantelte Werte für die Gesamtenergie des Elektrons:

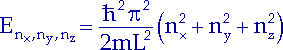
(12.11)

Dem Grundzustand ist mit n_x = n_y = n_z = 1 die Energie E _1,1,1 = ^2 2/2mL² zugeordnet. Der erste angeregte Energiezustand kann auf drei unterschiedliche Arten erreicht werden: mit n_x = 2 und n_y = n_z = 1; n_y = 2 und n_x = n_z = 1 oder n_z = 2 und n_x = n_y = 1. Diese drei Kombinationen von Quantenzahlen liefern zwar drei verschiedene Wellenfunktionen, jedoch dasselbe Energieniveau.

In einem Potentialwürfel werden quantenmechanische Zustände durch drei Quantenzahlen beschrieben. Angeregte Zustände gleicher Energie lassen sich durch drei verschiedene Kombinationen von Quantenzahlen realisieren. Solche energiegleiche Zustände werden als miteinander entartet bezeichnet.

Die Entartung ergibt sich aus der Symmetrie eines Würfels. Würden wir einen Potentialtopf mit unterschiedlich langen Kanten wählen, so würde kein Energiewert dem anderen gleichen.