Institut für Theoretische Informatik
Willkommen auf der Webseite des Instituts für theoretische Informatik. Unser Institut befasst sich mit den theoretischen Grundlagen der Informatik, dabei stehen hauptsächlich die folgenden Themen im Vordergrund:
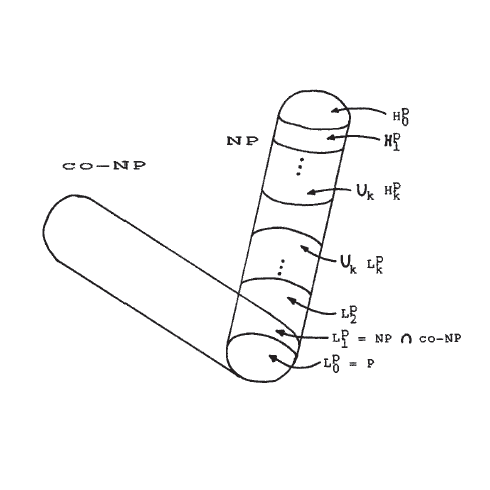
- Berechenbarkeit und Komplexitätstheorie
- Graphentheorie
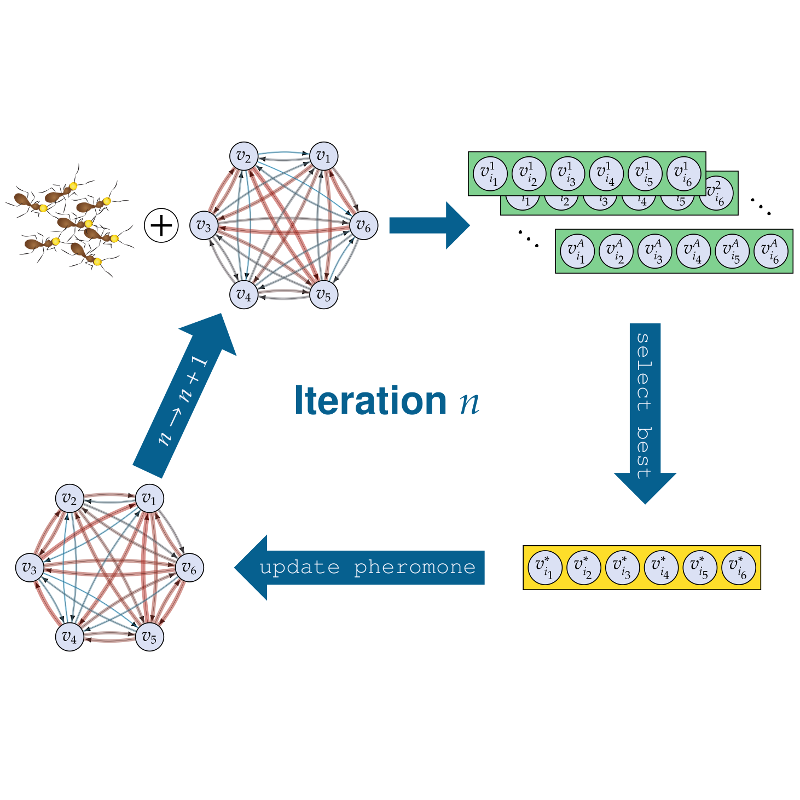
- Algorithmik und Datenstrukturen
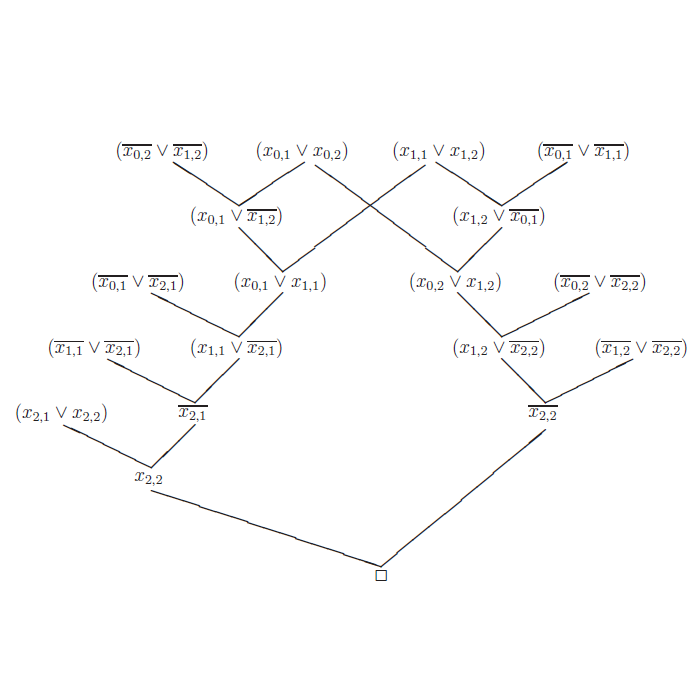
- Logik, speziell SAT-Solving
- Sequenzanalyse und Datenkompression
- Bioinformatik
- Quantum Computing
- Kryptologie
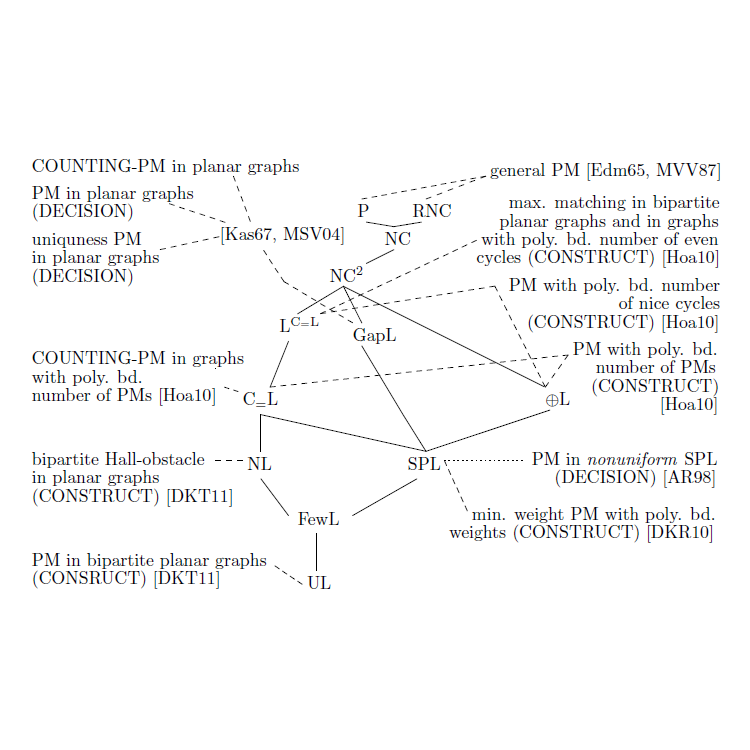
Neben diesen Schwerpunkten sind wir natürlich auch an anderen Aspekten der theoretischen Informatik interessiert. Einen ersten Eindruck des Instituts kann man anhand des Institutsposters oder der nebenstehenden Gallerie gewinnen - unsere Forschung in Bildern.
Vorträge
Nachfolgend sind vergangene und anstehende Vorträge aufgelistet. Sofern nicht anderst angegeben finden die Vorträge im Raum O27/531 statt.
12.12.2025 14:00 Nick Winter “Berechnung eines längsten gemeinsamen Teilstrings mithilfe von Suffix-Arrays”
12.12.2025 13:30 Hannes Schäuble “Backdoor Set Detection for Horn and Binary Clauses”
14.11.2025 13:30 Fabian Hausmann "Über die Komplexität von Monotoner Dualisierung"
01.08.2025 14:00 Eugen Nabiev “Untersuchung der Möglichkeiten zur Nutzung von Catalytic Space”
04.07.2025 13:30 Jonas Mayer "Graphtransformationen zur Bestimmung nicht-repetitiver Pfade und Zyklen"
13.06.2025 13:30 Mirko Landgraf "A Space-Efficient Data Structure for the Naming Function"
14.02.2025 14:15 Dawei Hu "Analyse einer Variante von Chomp aus Sicht der Spieltheorie"
14.02.2025 13:30 Tom Spänkuch "Calculating atomic distances in proteins through various data structures"
31.01.2025 13:30 Probevortrag Thomas Büchler "Pangenome Structures: Design, Construction, and Applications"
Kontakt
Institut für Theoretische Informatik
Universität Ulm
D-89069 Ulm
Telefon: +49 (0)731 50 24101
Telefax: +49 (0)731 50 1224101
Sekretariat
Raum: O27/537
Klausurtermine
Ersttermine:
Algorithmen und Datenstrukturen am 17.02.2026 ab 11:00 Uhr in H20,21,22,2,3
Grundlagen der theoretischen Informatik am 17.02.2026 ab 14:00 Uhr in H20,21,22,2,3
Einführung in die Bioinformatik am 20.02.2026 ab 09:00 Uhr in Raum O27/123
Zweittermine:
Algorithmen und Datenstrukturen am 31.03.2026 ab 09:00 Uhr in H20,21,22,4/5
Grundlagen der theoretischen Informatik am 31.03.2026 ab 12:00 Uhr in H20,21,22,1
Einführung in die Bioinformatik am 10.04.2026 ab 10:00 in Raum O27/123
Bitte beachten Sie: Prüfungsanmeldungen haben bei schriftlichen Prüfungen bis spätestens fünf Tage vor Prüfungsdatum zu erfolgen (z.B. Prüfungsdatum 21.02., letzte Anmeldemöglichkeit: 16.02.) Verspätete Anmeldungen sind nicht möglich.