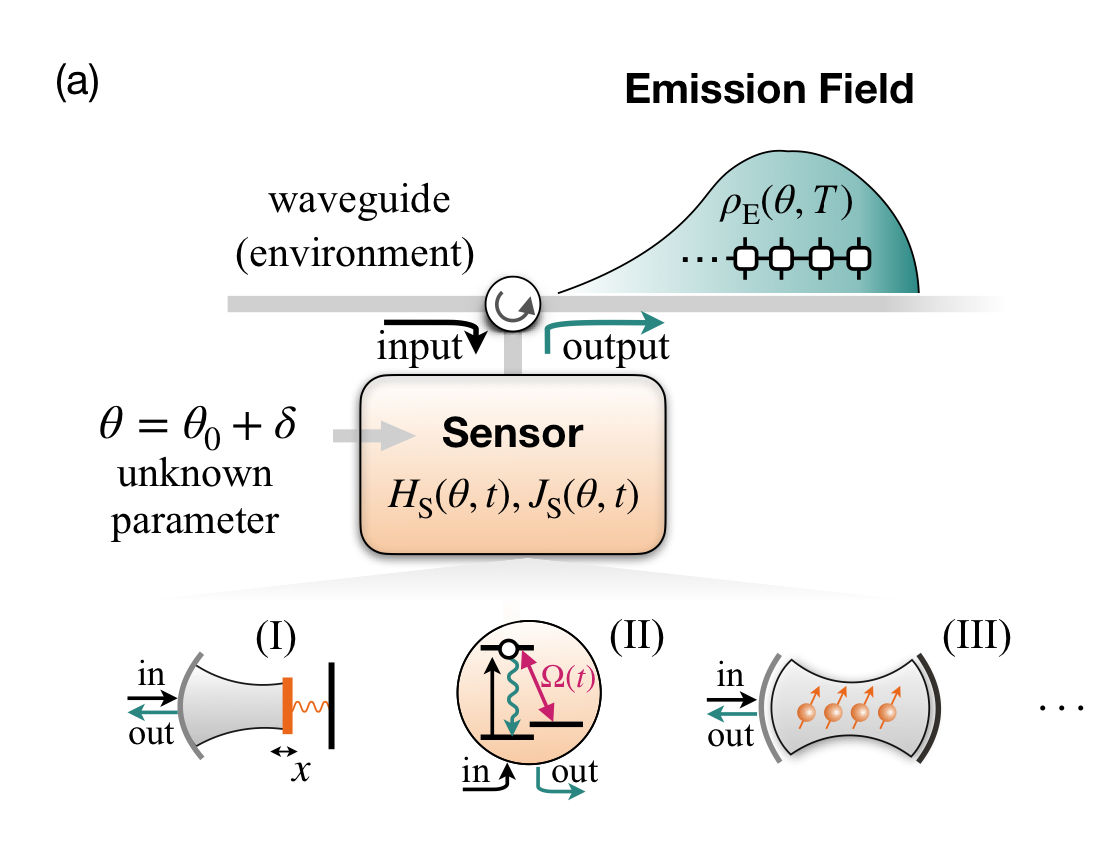
Efficient Information Retrieval for Sensing via Continuous Measurement, Dayou Yang , Susana F. Huelga , and Martin B. Plenio, Phys. Rev. X 13, 031012, arXiv:2209.08777
Continuous monitoring of driven-dissipative quantum-optical systems is a crucial element in the implementation of quantum metrology, providing essential strategies for achieving highly precise measurements beyond the classical limit. In this context, the relevant figure of merit is the quantum Fisher information of the radiation field emitted by the driven-dissipative sensor. Saturation of the corresponding precision limit as defined by the quantum Crame ́r-Rao bound is typically not achieved by conventional, temporally local continuous-measurement schemes such as counting or homodyning. To address the outstanding open challenge of efficient retrieval of the quantum Fisher information of the emission field, we design a novel continuous-measurement strategy featuring temporally quasilocal measurement bases as captured by matrix-product states. Such a measurement can be implemented effectively by injecting the emission field of the sensor into an auxiliary open system, a “quantum-decoder” module, which “decodes” specific input matrix-product states into simple product states as its output field, and performing conventional continuous measurement at the output. We devise a universal recipe for the construction of the decoder by exploiting the time-reversal transformation of quantum-optical input-output channels, thereby establishing a universal method to achieve the quantum Crame ́r-Rao precision limit for generic sensor designs based on continuous measurement. As a by-product, we establish an effective formula for the evaluation of the quantum Fisher information of the emission field of generic driven- dissipative open sensors. We illustrate the power of our scheme with paramagnetic open sensor designs including linear force sensors, fiber-interfaced nonlinear emitters, and driven-dissipative many-body sensors, and demonstrate that it can be robustly implemented under realistic experimental imperfections.
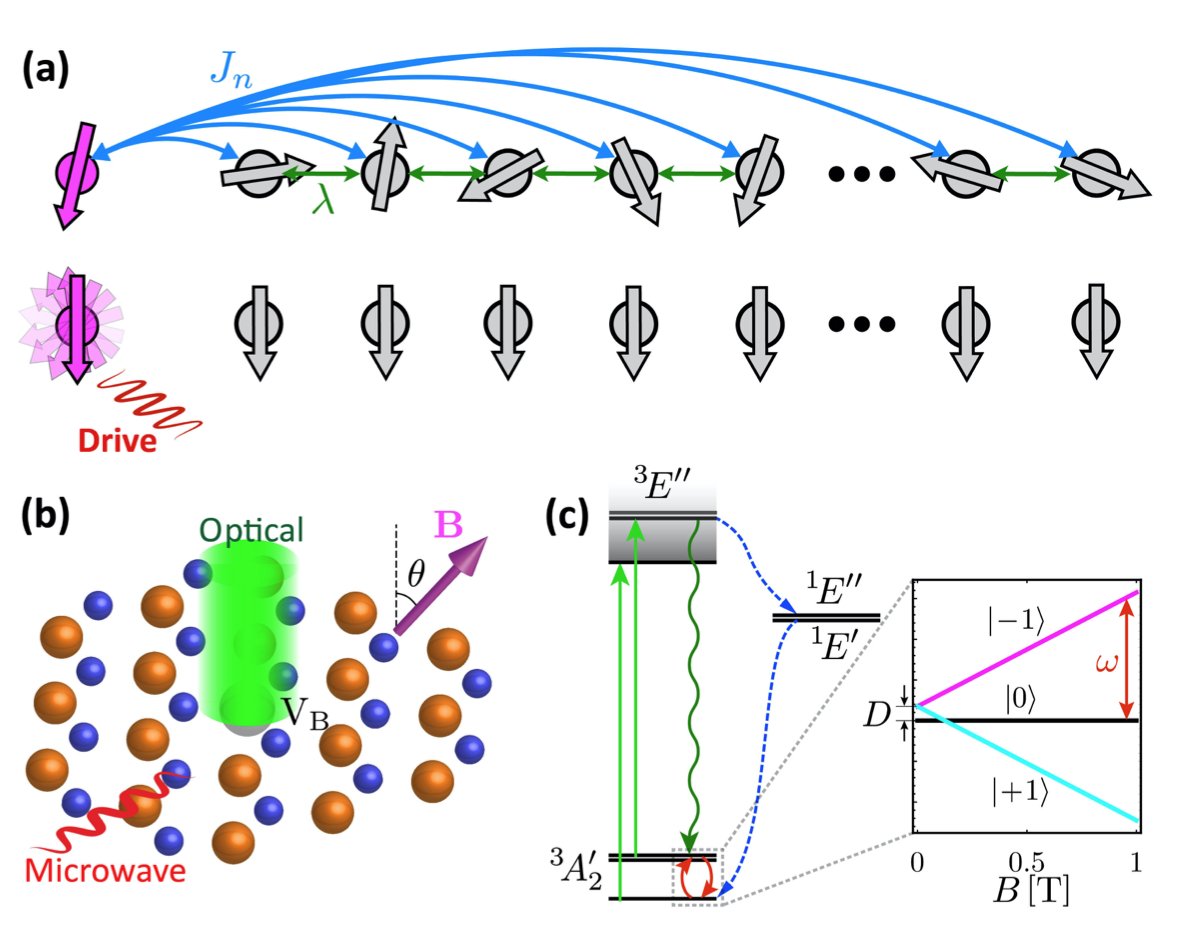
Active hyperpolarization of the nuclear spin lattice: Application to hexagonal boron nitride color centers, F. T. Tabesh, M. Fani, J. S. Pedernales, M. B. Plenio, and M. Abdi, Phys. Rev. B 107, 214307, arXiv:2010.03334
The active driving of the electron spin of a color center is known as a method for the hyperpolarization of the surrounding nuclear spin bath and to initialize a system with large number of spins. Here, we investigate the efficiency of this approach for various spin coupling schemes in a one-dimensional Heisenberg chain coupled to a central spin. To extend our study to the realistic systems with a large number of interacting spins, we employ an approximate method based on Holstein-Primakoff transformation. The validity of the method for describing spin polarization dynamics is benchmarked by the exact numerics for a small lattice, where the accuracy of the bosonic Holstein-Primakoff approximation approach is confirmed. We, thus, extend our analysis to larger spin systems where the exact numerics are out of reach. The results prove the efficiency of the active driving method when the central spin interaction with the spin bath is long range and the inter-spin interactions in the bath spins is large enough. The method is then applied to the realistic case of optically active negatively charged boron vacancy centers (VB) in hexagonal boron nitride. Our results suggest that a high degree of hyperpolarization in the boron and nitrogen nuclear spin lattices is achievable even starting from a fully thermal bath. As an initialization, our work provides the first step toward the realization of a two-dimensional quantum simulator based on natural nuclear spins and it can prove useful for extending the coherence time of the VB centers.
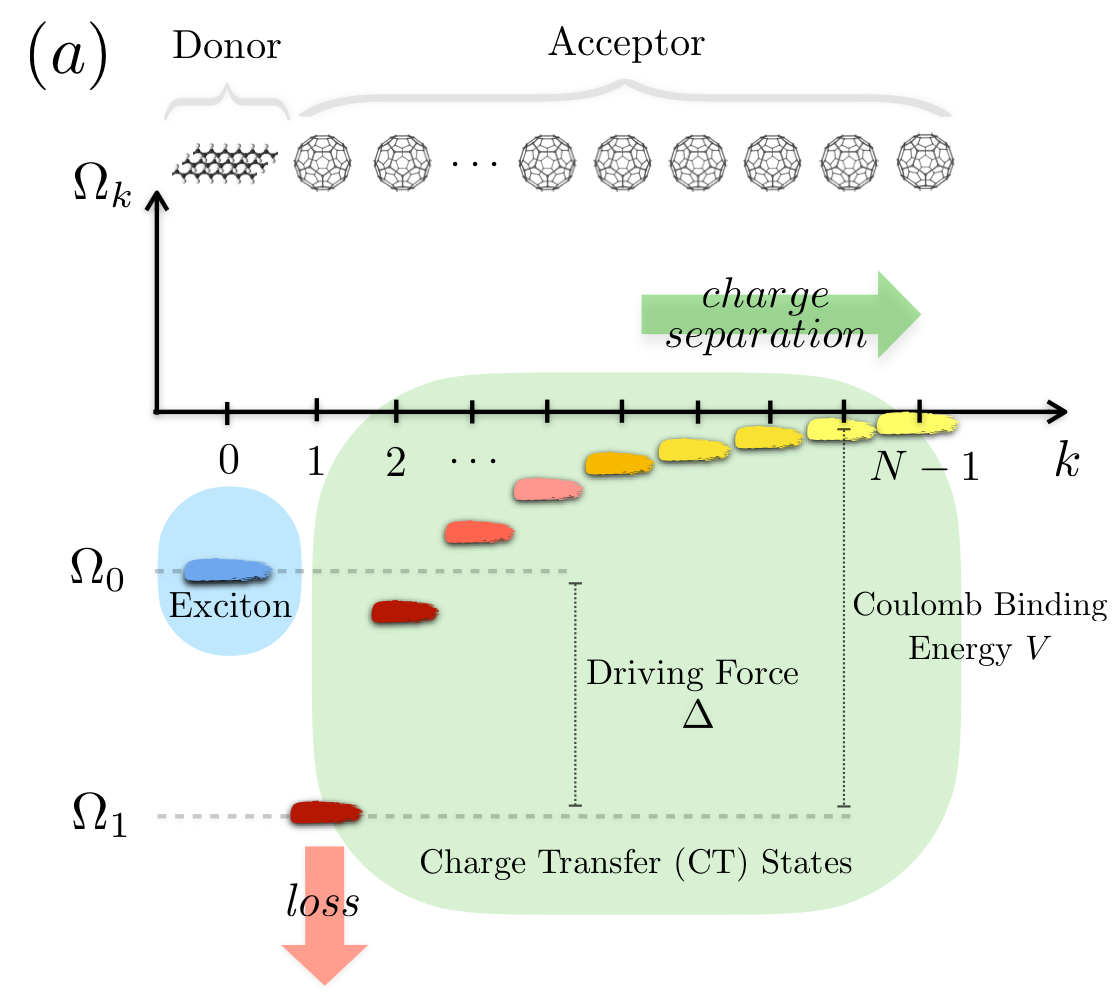
Driving force and nonequilibrium vibronic dynamics in charge separation of strongly bound electron–hole pairs, Alejandro D. Somoza, Nicola Lorenzoni, James Lim, Susana F. Huelga, and Martin B. Plenio, Commun Phys 6, 65 (2023), arXiv:2205.06623
Electron-hole pairs in organic photovoltaics efficiently dissociate although their Coulomb- binding energy exceeds thermal energy at room temperature. The vibronic coupling of electronic states to structured vibrational environments containing multiple underdamped modes is thought to assist charge separation. However, non-perturbative simulations of such large, spatially extended, electronic-vibrational (vibronic) systems remain an unmet challenge which current methods bypass by considering effective one-dimensional Coulomb potentials or unstructured environments where the effect of underdamped modes is ignored. Here we address this challenge with a non-perturbative simulation tool and investigate the charge separation dynamics in one, two and three-dimensional donor-acceptor networks to identify under what conditions underdamped vibrational motion induces efficient long-range charge separation. The resulting comprehensive picture of ultrafast charge separation differentiates electronic or vibronic couplings mechanisms for a wide range of driving forces and identifies the role of entropic effects in extended systems. This provides a toolbox for the design of efficient charge separation pathways in artificial nanostructures.
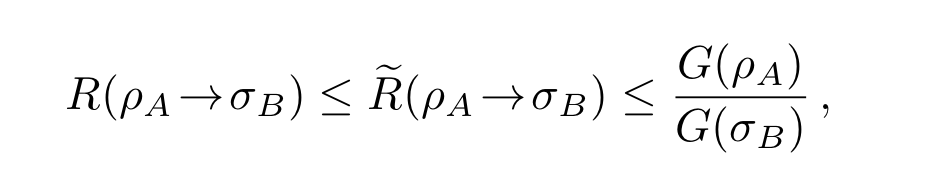
Asymptotic State Transformations of Continuous Variable Resources, Giovanni Ferrari, Ludovico Lami, Thomas Theurer, and Martin B. Plenio, Commun. Math. Phys. 398, 291–351 (2023), arXiv:2010.00044
We study asymptotic state transformations in continuous variable quantum resource theories. In particular, we prove that monotones displaying lower semicontinuity and strong superadditivity can be used to bound asymptotic transformation rates in these settings. This removes the need for asymptotic continuity, which cannot be defined in the traditional sense for infinite-dimensional systems. We consider three applications, to the resource theories of (I) optical nonclassicality, (II) entanglement, and (III) quantum thermodynamics. In cases (II) and (III), the employed monotones are the (infinite-dimensional) squashed entanglement and the free energy, respectively. For case (I), we consider the measured relative entropy of nonclassicality and prove it to be lower semicontinuous and strongly superadditive. One of our main technical contributions, and a key tool to establish these results, is a handy variational expression for the measured relative entropy of nonclassicality. Our technique then yields computable upper bounds on asymptotic transformation rates, including those achievable under linear optical elements. We also prove a number of results which guarantee that the measured relative entropy of nonclassicality is bounded on any physically meaningful state and easily computable for some classes of states of interest, e.g., Fock diagonal states. We conclude by applying our findings to the problem of cat state manipulation and noisy Fock state purification.
Spin-Dependent Momentum Conservation of Electron-Phonon Scattering in Chirality-Induced Spin Selectivity, Clemens Vittmann, James Lim, Dario Tamascelli, Susana F. Huelga, and Martin B. Plenio, J. Phys. Chem. Lett. 2023, 14, XXX, 340–346, arXiv:2209.05323
The elucidation of the mechanisms underpinning chiral-induced spin selectivity remains an out- standing scientific challenge. Here we consider the role of delocalized phonon modes in electron trans- port in chiral structures and demonstrate that spin selectivity can originate from spin-dependent energy and momentum conservation in electron-phonon scattering events. While this mechanism is robust to the specific nature of the vibrational modes, the degree of spin polarization depends on environmental factors, such as the specific temperature and phonon relaxation rates, as well as the presence of external driving fields. This parametric dependence is used to present experimentally testable predictions of our model.
