Contributors
H. Losert, and W.P. Schleich
Collaborations
D.M. Lee (Texas A&M University, College Station)
Funding
Texas A&M University Institute for Advanced Study (TIAS)
Coherence in liquid helium
In collaboration with David Lee (Texas A&M University, College Station, USA), we investigate the long-term spin dynamics in liquid helium. In a dilute \( ^3\rm{He}\)- \(^4\rm{He} \) mixture, the \( ^3\rm{He}\) atoms are weakly interacting and form a Fermi quantum gas, rather than a strongly interacting fluid. For such a liquid, it has been shown [1] by the group of D. Lee, that in a particular case, extremely long-lived oscillations (up to 10s) can be observed as shown in Fig. 1.
The setup consists of two interconnected chambers in a very strong homogeneous magnetic field, leading to a spin-polarization of \( ^3\rm{He}\). The spins in one of these chambers are flipped by a single \(\pi\)-pulse from a NMR-coil around this reservoir and the following free induction decay is recorded by the very same coil. The resulting signal shows a very clear typical quantum revival-like shape [3] as can be seen in the picture. One more remarkable feature of this setup is the internal "memory" of this system which in influences succeeding pulses up to a time of roughly 100 minutes.
Up to now, the origin of the signal and the corresponding internal processes in this fluid are unknown.
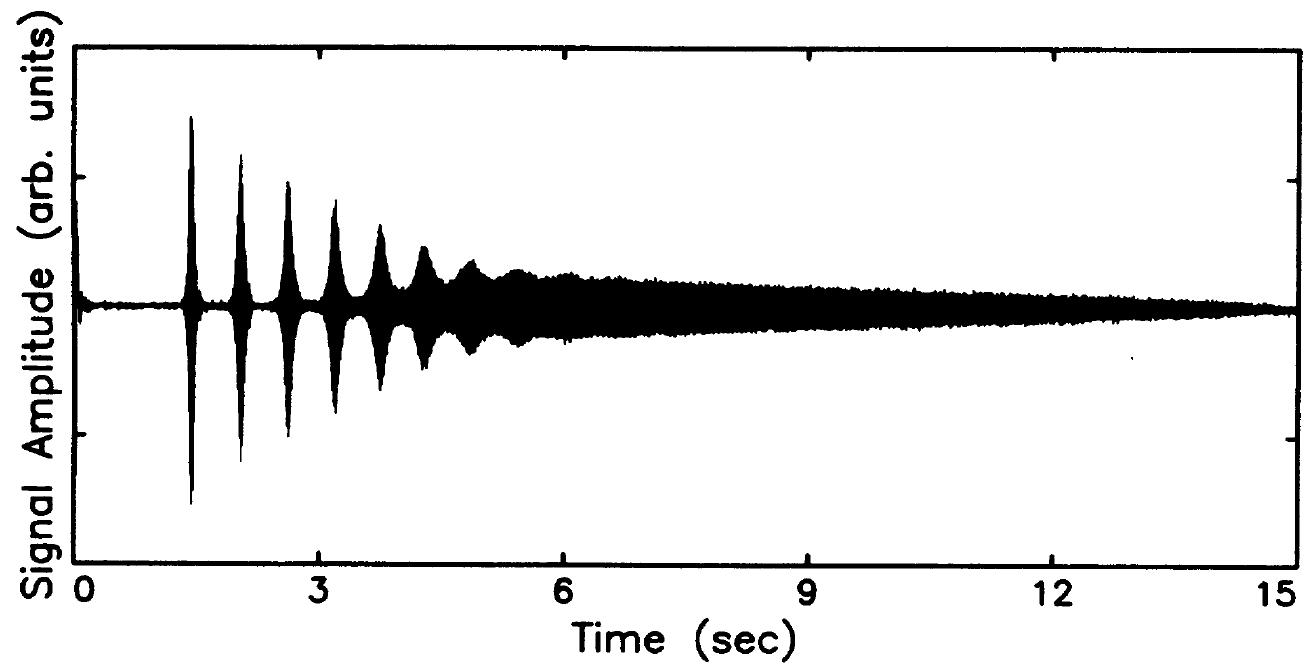
Fig. 1: Free-induction decay measured via an NMR coil following a spin-flip pulse in one chamber.
The dynamics of the magnetization \( \vec{M}(\vec{r},t) \) in such a Fermi system is described by the Leggett-equation [2] $$ \frac{\partial}{\partial t} \vec{M}-\vec{M}\times \gamma \delta\vec{H}=\frac{D_s}{1+\mu^2M^2}\left[\nabla\vec{M}+\mu(\vec{M}\times\nabla\vec{M})+\mu^2(\vec{M}\cdot\nabla\vec{M})\vec{M}\right].$$ This equation can be rewritten as a set of two coupled equations, one being a Schrödinger type equation, giving a first glimpse on the remarkable resemblance between the observed signal and quantum revivals. We are working on a simple and intuitive quantum mechanical model, able to reproduce the behavior of the system.
References
[1] G. Nunes, Jr., C. Jin, D. L. Hawthorne, A. M. Putnam, and D. M. Lee, Spin-polarized 3He-4He solutions: Longitudinal spin diffusion and nonlinear spin dynamics, Phys. Rev. B 46, 9082 (1992)
[2] A. J. Leggett, Spin diffusion and spin echoes in liquid 3 He at low temperature, J. Phys. C 3, 448 (1970)
[3] M. Fleischhauer and W.P. Schleich, Revivals made simple: Poisson summation formula as a key to the revivals in the Jaynes-Cummings model, Phys. Rev. A 47, 4258 (1993)