Ableitung der Planckschen Strahlungsformel nach Einstein

Bei dieser Ableitung werden wir auf Einsteins Photonenhypothese und das Bohrsche Atommodell vorgreifen. Einsteins Photonenhypothese ist die Annahme, dass Licht aus Teilchen besteht, den sogenannten Lichtquanten oder Photonen. Jedes Photon besitze die Energie .
Die Existenz diskreter Energiezustände für Elektronen in einem Atom, die wir erst im Bohrschen Atommodell kennenlernen, wird hier auch verwendet.

Wir betrachten zwei Energieniveaus in einem Atom, die sich um einen Energiebetrag unterscheiden, und zwar:

Zwischen zwei solchen Energieniveaus sind nach Einstein drei verschiedene Arten von Strahlungsübergängen möglich:

1. Absorption eines Lichtquantes bringt ein Elektron aus dem energetisch tieferen Zustand mit der Energie E ₁ in den energetisch höheren Zustand mit der Energie E ₂. Die dazu notwendige Energie E ₂ - E ₁ = wird dem Strahlungsfeld entzogen: absorbiert.
   
   
2. Spontane Emission ist der umgekehrte Vorgang zur Absorption. Ein Elektron geht spontan aus einem höheren in einen tieferen Energiezustand über. Dabei wird ein Lichtquant abgestrahlt: emittiert.
   
   
3. Induzierte Emission oder stimulierte Emission tritt ein, wenn ein Photon aus dem Strahlungsfeld eine Emission erzwingt. Ein Elektron kehrt dabei aus einem höheren in einen tieferen Energiezustand zurück. Die Energie des eingestrahlten Photons muss gleich der Energiedifferenz dieser Zustände sein. So werden zwei gleiche Photonen emittiert: das eine aus dem Energieunterschied wie bei der spontanen Emission und das andere aus der Anregung. (Auf der induzierten Emission basiert das Laserprinzip. In Lasern initiieren einzelne Photonen die Emission vieler gleicher Photonen.)
   
   

Im Bild unten werden diese Prozesse schematisch illustriert:

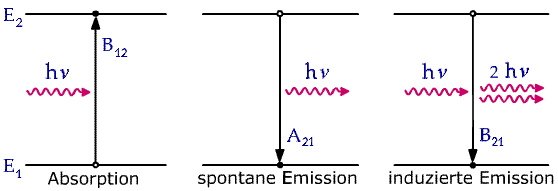
Nun betrachten wir ein System von N Atomen in einem schwarzen Körper. Die Anzahl der Elektronen im Zustand E ₁ sei N₁ und die Anzahl der Elektronen im Zustand E ₂ sei N₂. Die Zahl N₁ bzw. N₂ nennen wir im Folgenden die Besetzungszahl des Zustands E ₁ bzw. E ₂. Als Teil eines schwarzen Körpers steht das System im Gleichgewicht mit einem elektromagnetischen Feld der Energiedichte u().  Deswegen erfolgen gleich viele Elektronenübergänge von E ₁ nach E ₂ wie von E ₂ nach E ₁ pro Zeiteinheit:

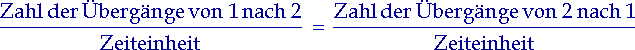
(2.1)

Diese Prozesse können mathematisch beschrieben werden:

Übergänge von 1 nach 2: Absorptionen:
Die Zahl der Übergänge von 1 nach 2 pro Zeiteinheit ist der Energiedichte u() und der Besetzungszahl N₁ proportional:

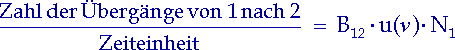
(2.2)

Der Proportionalitätsfaktor B₁₂ heißt Einstein-Koeffizient. Er zeigt die Wahrscheinlichkeit eines Übergangs pro Zeit- und Energiedichte-Einheit an.

Übergänge von 2 nach 1: Spontane Emissionen und Induzierte Emissionen:
Die Zahl der Übergänge von 2 nach 1 pro Zeiteinheit setzt sich aus zwei Termen zusammen:

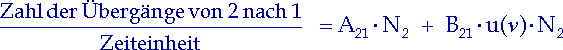
(2.3)

Der erste Term: A₂₁  N₂ ist die Zahl spontaner Emissionen und
der zweite Term: B₂₁  u()  N₂ ist die Zahl induzierter Emissionen je Zeiteinheit.
A₂₁ und B₂₁ sind ebenfalls Einstein-Koeffizienten.
Wegen (2.1) (thermisches Gleichgewicht) ist die Zahl der Absorptionen gleich der Zahl der Emissionen:

(2.4)

Wir lösen diese Gleichung nach dem Verhältnis der Besetzungszahlen auf:

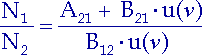
(2.5)

In der statistischen Thermodynamik wird die Verteilung der Teilchen des Gesamtsystems auf die verschiedenen möglichen Energieniveaus mit Hilfe der Boltzmann-Verteilungsfunktion beschrieben, so dass gilt:
Im thermischen Gleichgewicht verhalten sich die Besetzungszahlen N₁ und N₂ zueinander wie zu :

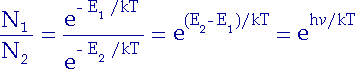
(2.6)

Gleichsetzen von (2.5) und (2.6) führt zu

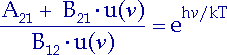
(2.7)

und Auflösen nach u() zu

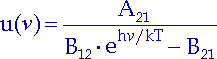
(2.8)

Für muss auch die Energiedichte beliebig groß werden: u() .
Der Einsteinkoeffizient A₂₁ ist endlich, deswegen wird der Nenner in (2.8) gegen Null gehen:

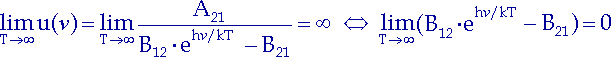
und wegen

folgt:

(2.9)

Diese Erkenntnis wenden wir in (2.8) an:

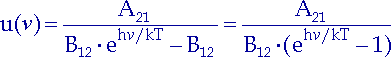
(2.10)

Das Verhältnis der verbleibenden Einsteinkoeffizienten erhalten wir durch Vergleich dieser Formel bei sehr kleinen Frequenzen mit dem Rayleigh-Jeans-Gesetz.

Mit der Reihenentwicklung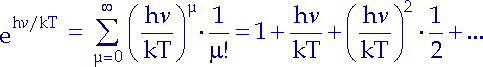

können wir für sehr kleine Frequenzen alle Summanden nach /kT vernachlässigen:

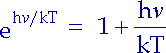
Das setzen wir in (2.10) ein: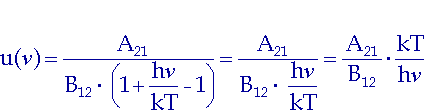

(2.11)

Nach Vergleich dieser Formel mit dem Rayleigh-Jeans-Gesetz: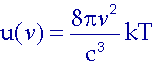

ergibt sich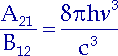

(2.12)

und schließlich die Plancksche Strahlungsformel:

Plancksche Strahlungformel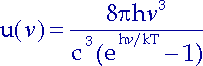

Einstein hat mit seiner Herleitung der Planckschen Strahlungsformel einen sehr starken Hinweis für die Existenz der Quanten der Energie gegeben.