Herleitung: Bei den beiden Gleichungen von Gay-Lussac und Boyle-Mariotte war immer eine Variable, im ersten Fall der Druck, im zweiten die Temperatur gleichbleibend (=konstant). Um jedoch uneingeschränkt rechnen zu können, braucht man eine Gleichung, die den Zusammenhang zwischen allen drei Größen (Druck, Temperatur und Volumen) beschreibt. Dazu muss man die Gesetze von Gay-Lussac und Boyle-Mariotte zusammenfassen. 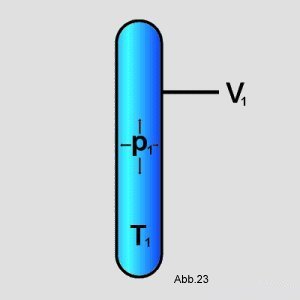Man geht von einem System aus, das eine Temperatur T₁, einen Druck p₁ und ein Volumen V₁ hat: Der Druck wird verändert auf p₂ und die Temperatur auf T₂. Die Frage ist: Wie sieht dann das Volumen V₂ aus?

Im ersten Schritt wird der Druck von p₁ auf p₂ geändert. Die Temperatur wird dabei gleich gehalten. Folglich läßt sich das Gesetz von Boyle-Mariotte anwenden. Man benützt dazu Formel (10) und löst diese nach V_x auf (Im graphischen Beispiel wird der Druck erhöht):

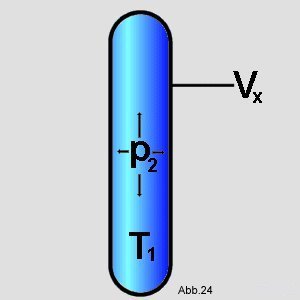
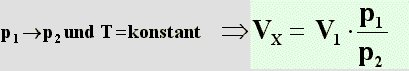(11)

Danach hält man den neuen Druck p₂ konstant und verändert nur die Temperatur von T₁ auf T₂. Dieser Vorgang läßt sich durch das Gesetz von Gay-Lussac berechnen. Man benützt dazu Formel (7) (Im graphischen Beispiel wird die Temperatur erhöht):

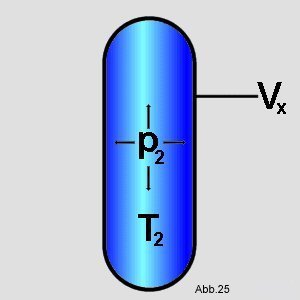
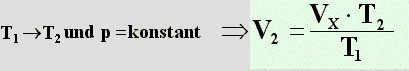
(12)

In die zweite Gleichung setzt man V_x aus der ersten Gleichung ein, und erhält folgendes:

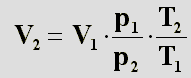
(13)

Umgestellt ergibt sich:

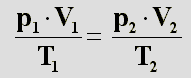
(14)

Daraus folgt weiterhin, daß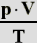

konstant ist.

Man weiß nun, daß das Produkt aus Volumen und Druck auf die Temperatur bezogen einen konstanten Wert hat. Um diesen berechnen zu können, benötigt man die drei zusammenhängenden Werte an einem bestimmten Punkt. Als Bezugszustand kann man den eines idealen Gases bei einem Druck von 1,013 bar und einer Temperatur von 273,15 K (= 0°C) wählen. An diesem Punkt beträgt nach Avogadro das Volumen eines Mols eines idealen Gases 22,414 l (= 22,414 dm³). Deswegen muss man noch die Stoffmenge n einbeziehen, damit man die molaren Verhältnisse erhält. Diese Werte werden mit der 0 als Index versehen, da sie sich auf den Punkt bei 0°C beziehen.
Man kann sie nun in die Gleichung einsetzen und erhält:

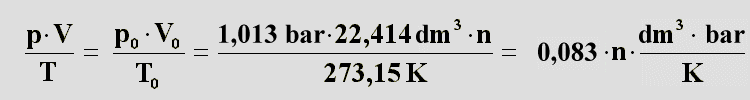
(15)

Die grün unterlegte Zahl und die Einheiten dahinter sind immer gleich, egal welchen Punkt man betrachtet hat. Sie sind die Konstante die R genannt wird und den Namen "Allgemeine Gaskonstante" trägt. Nun kann man das ideale Gasgesetz formulieren:

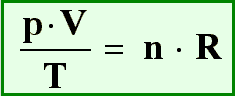
(16)

Beispiel:
Man läßt 2 mol Sauerstof O₂ in ein umgekehrtes, mit Wasser gefülltes Gefäß blubbern:



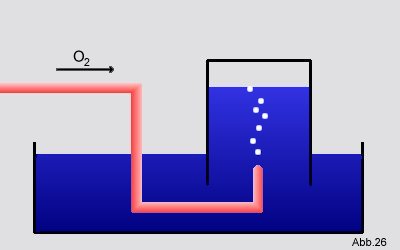Gegeben: Die Außentemperatur beträgt 25°C und der Luftdruck 1,013 bar.

Frage: Wie groß ist das Volumen, das der Sauerstoff einnehmen wird?

Lösung: Hier kann man das ideale Gasgesetz anwenden. Es lautet wie folgt:



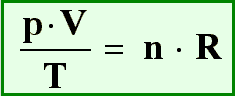
Die Stoffmenge n ist 2 mol, die Temperatur beträgt 298K (25°C + 273) und der Druck beträgt 1,013 bar (normaler Luftdruck). Außerdem benötigt man noch den Wert der allgemeinen Gaskonstante R. Er beträgt: 0,083 (cm³ * bar) / K (siehe Formel (15)). Diese Werte setzt man nun in die Formel ein:



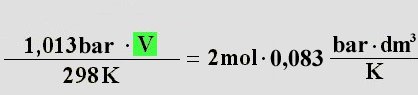
Diese löst man nun nach dem Volumen V auf:



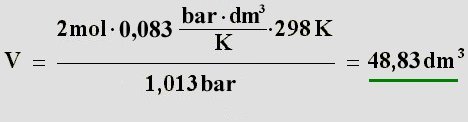Antwort: Es ergibt sich ein Sauerstoffvolumen von 48,83 dm³ bzw. Liter (1 dm³ = 1 Liter).