Algebra and Number Theory
The research at the Institute of Pure Mathematics is centered around algebraic geometry and number theory, especially in their fruitful synthesis called arithmetic geometry.
The research is arithmetic geometry in the institute is centered around algebraic curves over number fields. Here you can think of hyperelliptic curves, such as that defined by
y2 = x6 + x + 1,
but also of more general curves of higher genus such as plane quartic curves. An example of such a plane quartic is the Klein quartic, which is defined by the homogeneous equation
x3 y + y3 z + z3 x = 0.
A complex uniformization of this curve is depicted on the right.
Describing the geometric and number-theoretic properties of algebraic curves is a main goal of our research. Here are its main themes.
Moduli of curves
This theme is centered around the moduli space of curves of a given genus, and the reconstruction of curves from their invariants. Other subjects include generalizations of these moduli spaces, such as Hurwitz spaces and Teichmüller curves, as well as the question of descent, that is, when a curve can be defined over the field generated by its invariants.
p-adic aspects and the reduction of curves and covers
This includes the study of rigid geometry, as well as the calculation of the conductor exponent of an algebraic curve at a given prime, which encodes rather fine arithmetic information concerning the reduction properties of that curve.
Jacobians of curves and their endomorphisms
This includes the study of curves with real multiplication. At present a main topic of study is the explicit decomposition of general Jacobians into simple parts, as well as, conversely, to glue given Jacobians of curves together via torsion.
Explicit aspects and computer algebra
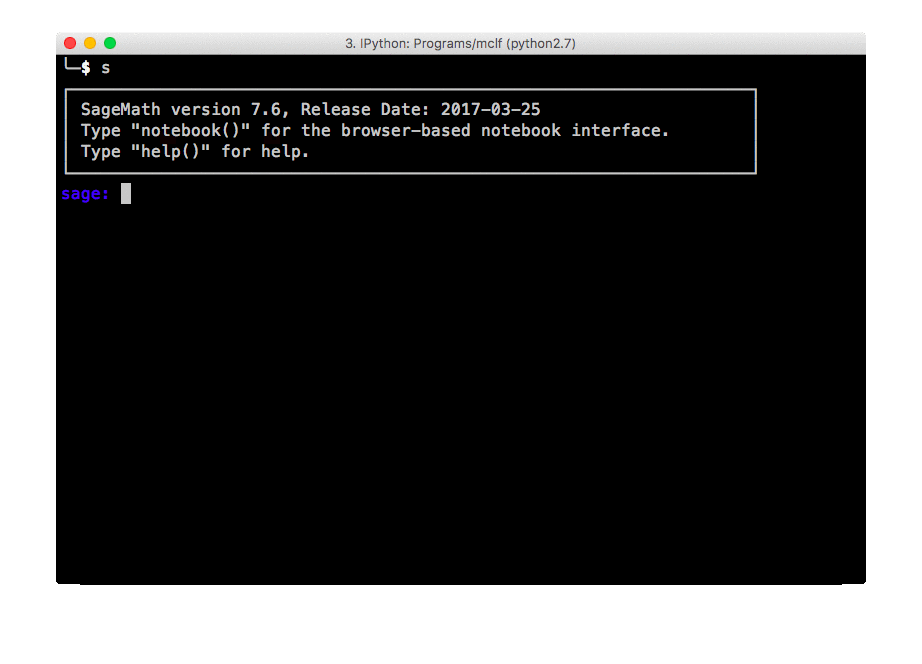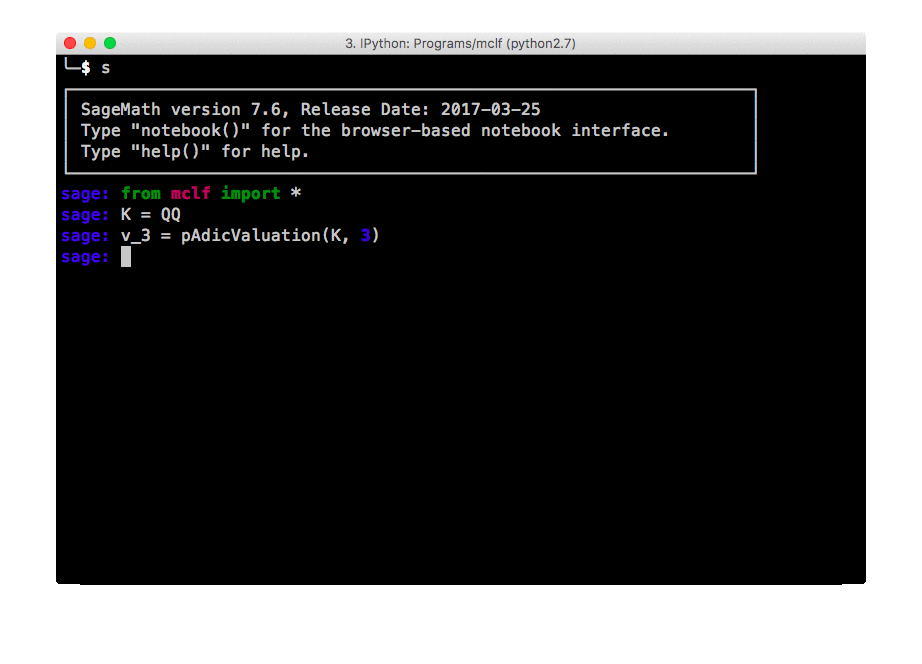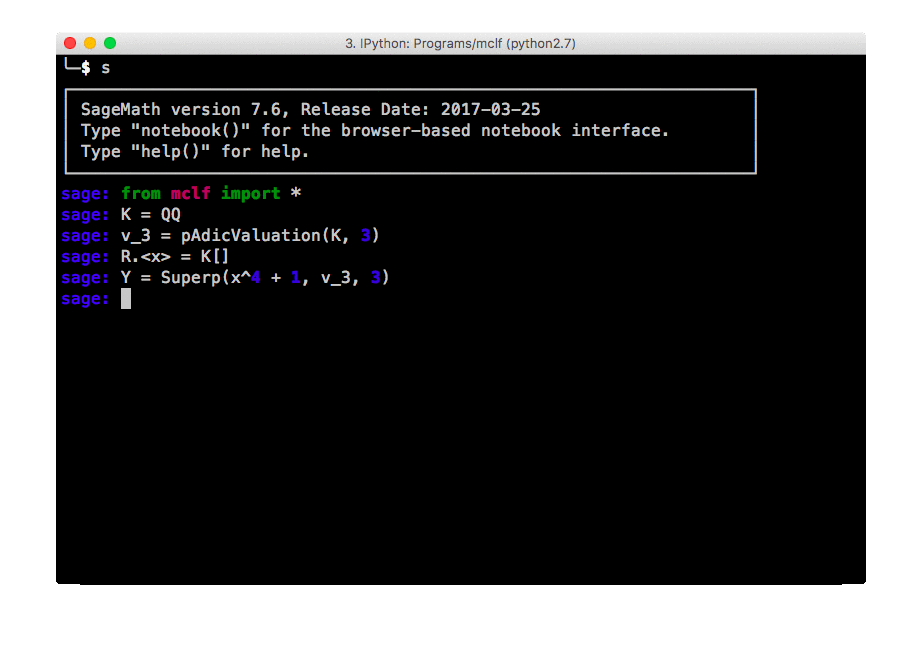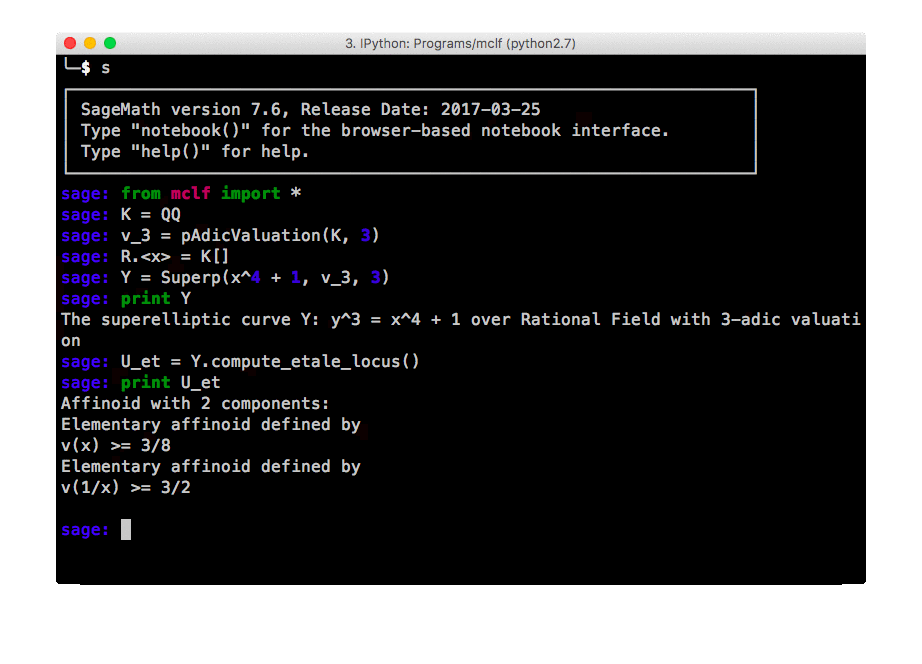
Explicit aspects play an important role in all of these works. The goal is not only to give theoretical answers and construction, but also to show how these can be implemented, and often to write these implementations in computer algebra systems such as SageMath. For example, the animation next to this text shows a package by Bouw and Wewers at work, which builds upon work of Julian Rüth. It studies the reduction properties of an algebraic curve given by explicit equations.
Research themes
- Arithmetic geometry (Bouw, Sijsling, Wewers)
- Computer Algebra (Sijsling)
Research projects
- L-functions and semistable reduction
- Moduli and descent of algebraic curves
- Motives and Diophantine equations
- Lifting problems
Collaborations and third party funding
- DFG priority program SPP 1489
- WIN
- Juniorprofessuren-Programm MWK Baden-Württemberg 2016: "Endomorphismen algebraischer Kurven"
- PICS JADERE (with Reynald Lercier, Elisa Lorenzo García and Christophe Ritzenthaler; sponsored by the French CNRS)
- DFG Sachbeihilfe 438058067 "Abstieg algebraischer Kurven"