2021
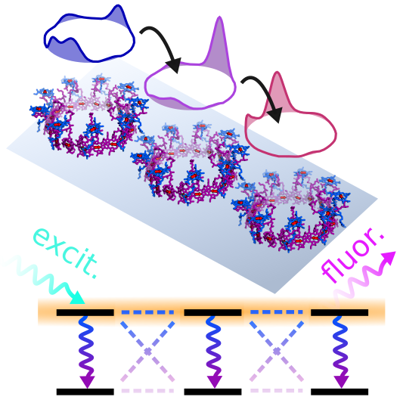
Design Principles for Long-Range Energy Transfer at Room Temperature, A.Mattioni, F. Caycedo-Soler, S. F. Huelga, and M. B. Plenio, Phys. Rev. X 11, 041003
DOI: doi.org/10.1103/PhysRevX.11.041003
The more efficiently a molecule absorbs light, the more strongly it will fluoresce. While crucial for some applications, this feature is highly detrimental for tasks relying on efficient transport and storage of harvested solar energy, such as photosynthesis or photovoltaics, limiting the distance across which energy can be transported before it is lost to the environment. Based on theoretical analysis of an exactly solvable model and extensive numerical simulations of quasi-1D arrays of bacterial pigment-protein complexes, we show how robust quantum interference between few pigments can be harnessed to allow energy to flow for much greater distances than previously thought possible, before being lost as heat or radiated as photons. When pigment-protein complexes are tightly packed, dark states (i.e. delocalized states that effectively decouple from the environment) participate in the energy transfer dynamics, speeding up the diffusion of excitons (tightly bound electron-hole pairs). At the same time, vibrationally-driven fast relaxation to low-energy excitonic states, protects the exciton from non-radiative recombination, thus extending the time available for energy transfer. Piecing together all these processes in a realistic model, we are able to reproduce yet unexplained experimental measurements, and provide guidelines to optimize energy transfer in novel light-harvesting technologies.
Versatile Atomic Magnetometry Assisted by Bayesian Inference, R. Puebla, Y. Ban, J.F. Haase, M.B. Plenio, M. Paternostro, and J. Casanova, Phys. Rev. Applied 16, 024044
DOI: doi.org/10.1103/PhysRevApplied.16.024044
Efficient construction of matrix-product representations of many-body Gaussian states, A. Nüßeler, I. Dhand, S.F. Huelga, and M.B. Plenio, Phys. Rev. A 104, 012415 (2021)
DOI: doi.org/10.1103/PhysRevA.104.012415
One-shot manipulation of entanglement for quantum channels, H.-J. Kim, S. Lee, L. Lami, and M.B. Plenio, IEEE Trans. Inf. Theo. 67, 5339 (2021)
DOI: doi.org/10.1109/TIT.2021.3079938
Enhanced force sensitivity and entanglement in periodically driven optomechanics, F. Cosco, J.S. Pedernales, and M.B. Plenio, Phys. Rev. A 103, L061501 (2021)
DOI: doi.org/10.1103/PhysRevA.103.L061501
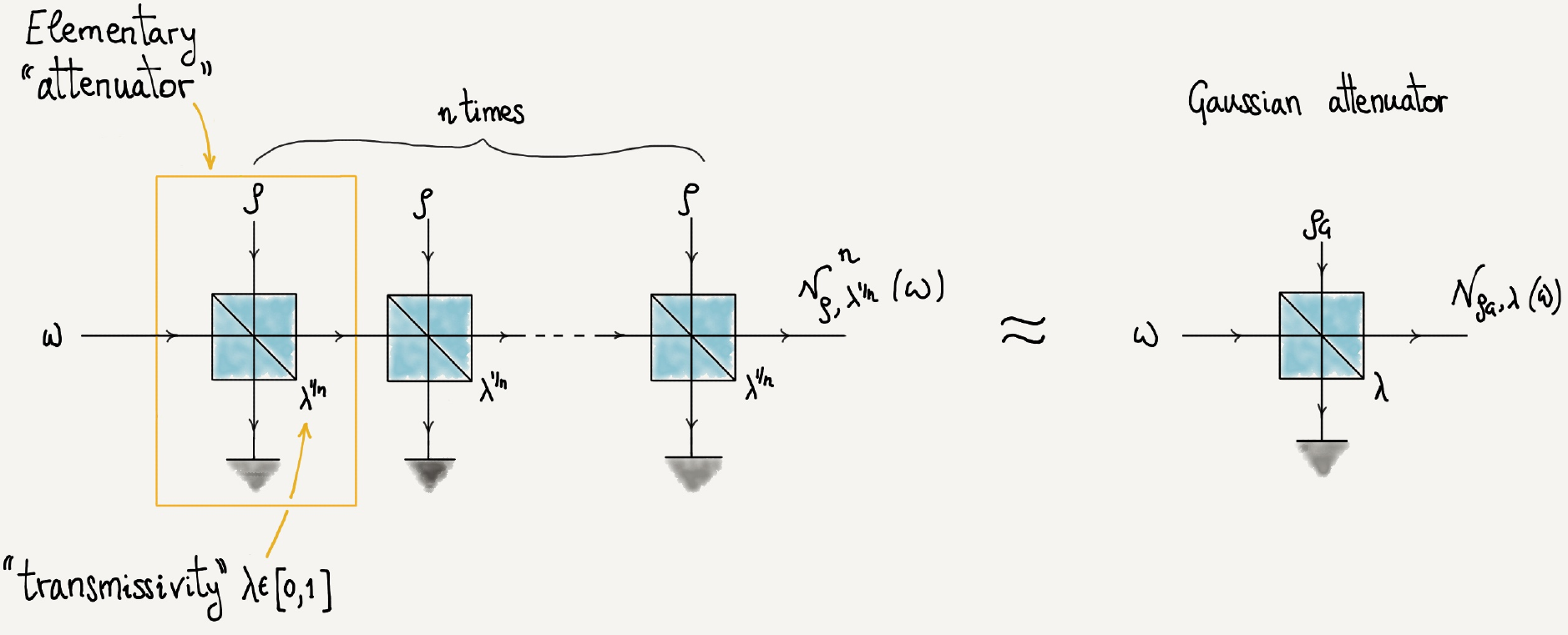
Convergence rates for the quantum central limit theorem, S. Becker, N. Datta, L. Lami, and C. Rouzé, Commun. Math. Phys. 383 (2021) 223–279
DOI: https://doi.org/10.1007/s00220-021-03988-1
Suppose that you have a long optical fibre, over which you try to send a quantum message. The fibre is immersed in a noisy environment (possibly including other active components of your quantum circuit), and occasionally a photon coming from it can make its way into the fibre and disturb the transmitted signal. How can we model the overall process? A celebrated “quantum central limit theorem” due to Cushen and Hudson implies that in the limit where the number n of i.i.d. elementary interactions with the environment tends to infinity the overall process amounts to a very simple thermal attenuator, under very general assumptions on the environment’s state. But how fast does this convergence take place? Here we prove, among other things, that the Hilbert-Schmidt norm distance between the effective environment state and the thermal state tends to zero at a rate inversely proportional to the square root of n, whenever the third moments of the initial environment’s state are finite. Via analytical and numerical examples we show that our results are tight in many respects. This allows us to establish bounds on the classical and quantum capacities of the quantum channel modelling the above optical fibre.
Energy-constrained discrimination of unitaries, quantum speed limits and a Gaussian Solovay-Kitaev theorem, S. Becker, N. Datta, L. Lami, and C. Rouzé, Phys. Rev. Lett. 126, 190504,
DOI: https://doi.org/10.1103/PhysRevLett.126.190504
How much energy do you need to discriminate two unitary quantum channels? And how much entanglement? Here we investigate these questions and establish a number of results. First, we prove that optimal discrimination between two unitary channels in the presence of an energy constraint does not require the use of any entanglement. In practice, this means that the resources needed to achieve optimal discrimination are substantially reduced. Extending a result by Acín, we also show that a finite number of parallel queries suffices to achieve zero error discrimination even in this energy-constrained setting. Secondly, we employ mathematical tools known as energy-constrained diamond norms to study a novel type of quantum speed limits, which apply to pairs of quantum dynamical semigroups. These results answer the question of how fast one can guess the Hamiltonian a system is subjected to given its initial mean energy. Thirdly, we establish a version of the Solovay-Kitaev theorem that applies to the group of Gaussian unitaries over a finite number of modes, with the approximation error being measured with respect to the energy-constrained diamond norm relative to the photon number Hamiltonian. This theorem allows us to efficiently compile continuous variable quantum circuits.
Coherence of operations and interferometry, M. Masini, T. Theurer, and M. B. Plenio, Phys. Rev. A 103, 042426
DOI: doi.org/10.1103/PhysRevA.103.042426
Quantum coherence is at the core of many quantum properties that are believed to lead to quantum advantages in fields such as computation, communication, simulation, and sensing. Therefore, it is considered a resource and characterized with the help of quantum resource theories. An application of the resulting framework to concrete technological tasks is however non-trivial and largely missing. In this work, we address this gap and connect how well operations can detect or create coherence (as quantified from a resource theoretical perspective) to the performance of interferometric experiments that rely on these operations.
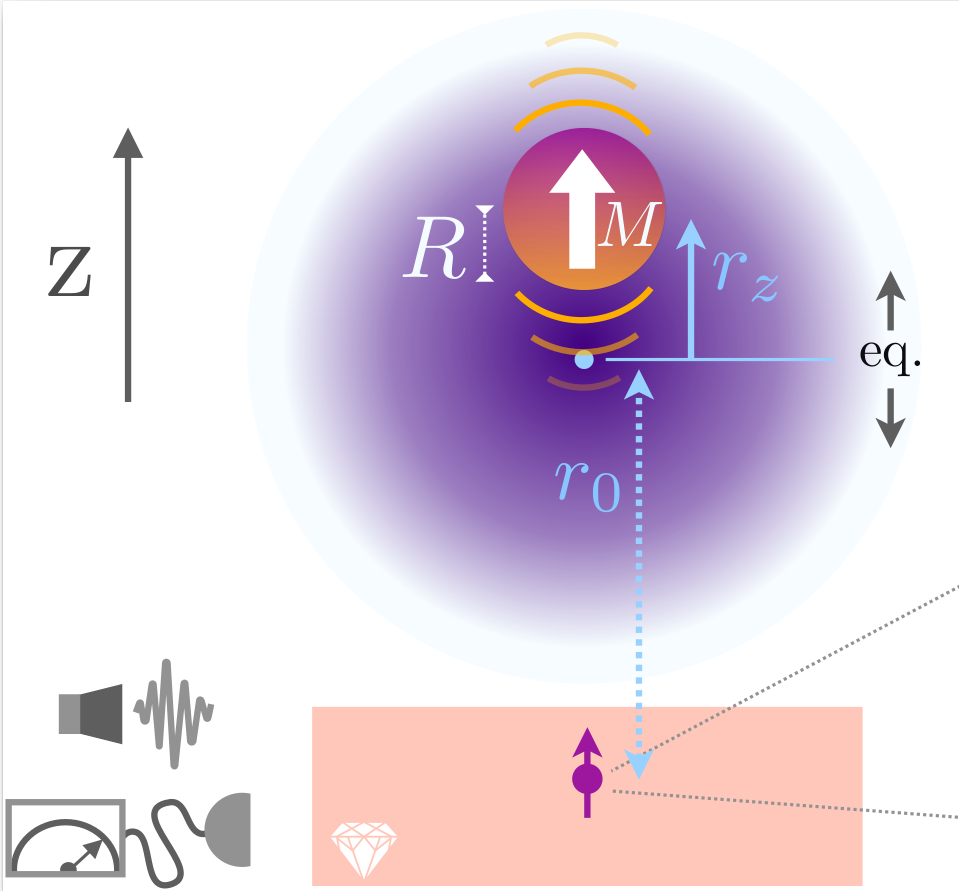
Ground-State Cooling of Levitated Magnets in Low-Frequency Traps, K. Streltsov, J. S. Pedernales, and M. B. Plenio, Phys. Rev. Lett. 126, 193602
DOI: doi.org/10.1103/PhysRevLett.126.193602
The ability to operate massive particles in the quantum regime is predicted to bring exceptional enhancements in sensitivity for metrological applications, and enable fundamental tests of the nature of the gravitational interaction. Such control can be reached via cooling the particles to their quantum mechanical ground state. With increasing mass this turns into a progressively harder task. In this work we present a feedback cooling scheme that is capable of reaching the ground state of trapped magnetic particles with radii in the range of 1-10um.
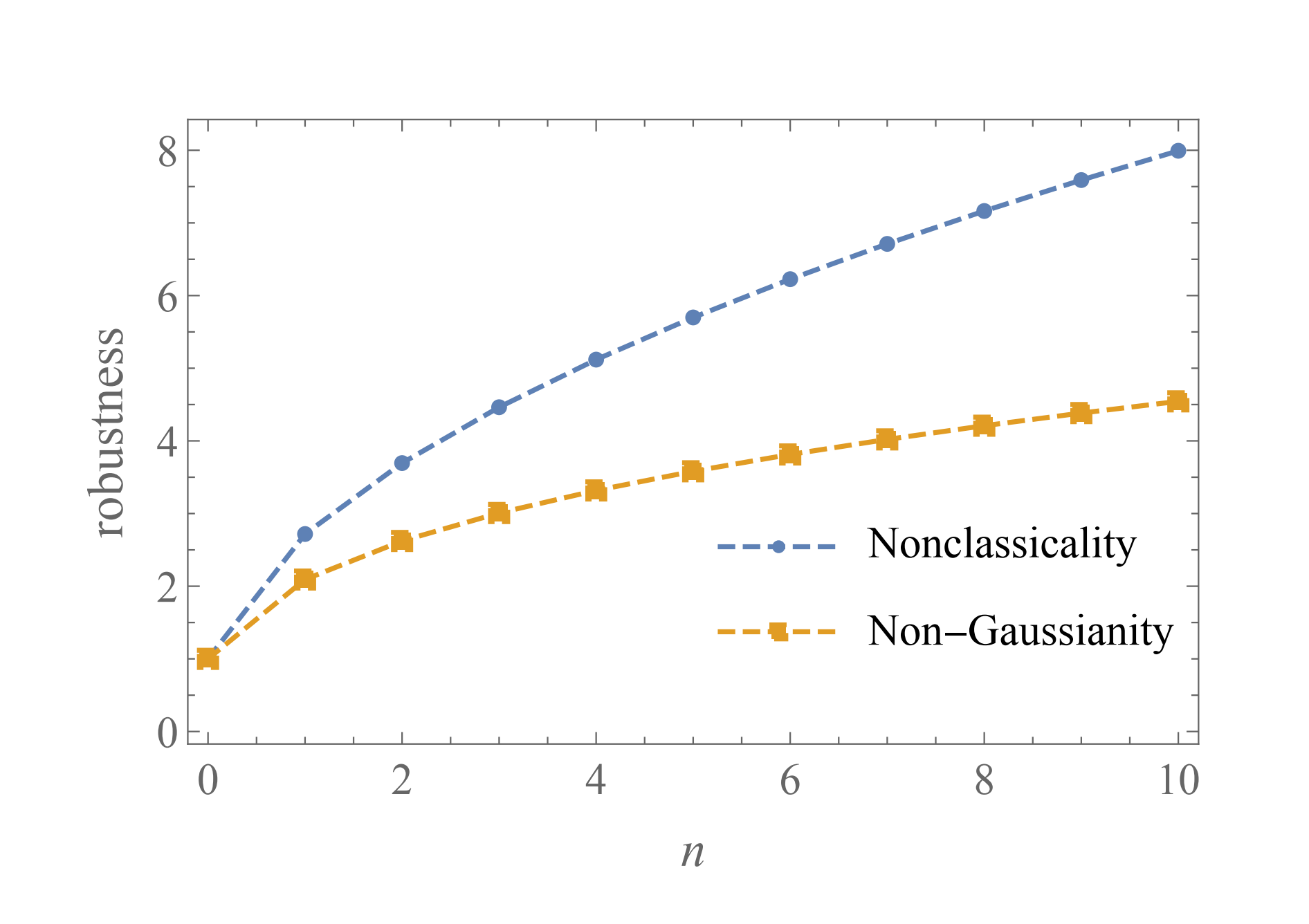
Framework for resource quantification in infinite-dimensional general probabilistic theories, L. Lami, B. Regula, R. Takagi, and G. Ferrari, Phys. Rev. A 103, 032424
DOI: doi.org/10.1103/PhysRevA.103.032424
It is well established that several features of quantum mechanical systems with no classical counterparts can be exploited as resources in practical applications, such as communication, computation, sensing and cryptography. It is then of paramount importance to rigorously quantify such an advantage, especially in relation to some explicit task that one might want to perform in a realistic scenario. In these two papers, we study the (generalized) robustness as a measure of a very large family of generic quantum resources, and its relation with a key task in quantum information: quantum channel discrimination. In particular, we prove that the robustness precisely quantifies the maximum advantage given by a resourceful state with respect to any free one, when used as a probe to determine which physical evolution it underwent. Our framework can be applied well beyond standard finite-dimensional quantum theory, and in particular, to all finite- and infinite-dimensional general probabilistic theories, i.e., generalizations of quantum mechanics itself. This is interesting both from a fundamental and practical perspective, as many resources needed for quantum technologies, e.g. nonclassicality and non-Gaussianity, are peculiar of systems with an associated infinite-dimensional Hilbert space.

Operational Quantification of Continuous-Variable Quantum Resources, B. Regula, L. Lami, G. Ferrari, and R. Takagi, Phys. Rev. Lett. 126, 110403,
DOI: doi.org/10.1103/PhysRevLett.126.110403
It is well established that several features of quantum mechanical systems with no classical counterparts can be exploited as resources in practical applications, such as communication, computation, sensing and cryptography. It is then of paramount importance to rigorously quantify such an advantage, especially in relation to some explicit task that one might want to perform in a realistic scenario. In these two papers, we study the (generalized) robustness as a measure of a very large family of generic quantum resources, and its relation with a key task in quantum information: quantum channel discrimination. In particular, we prove that the robustness precisely quantifies the maximum advantage given by a resourceful state with respect to any free one, when used as a probe to determine which physical evolution it underwent. Our framework can be applied well beyond standard finite-dimensional quantum theory, and in particular, to all finite- and infinite-dimensional general probabilistic theories, i.e., generalizations of quantum mechanics itself. This is interesting both from a fundamental and practical perspective, as many resources needed for quantum technologies, e.g. nonclassicality and non-Gaussianity, are peculiar of systems with an associated infinite-dimensional Hilbert space.
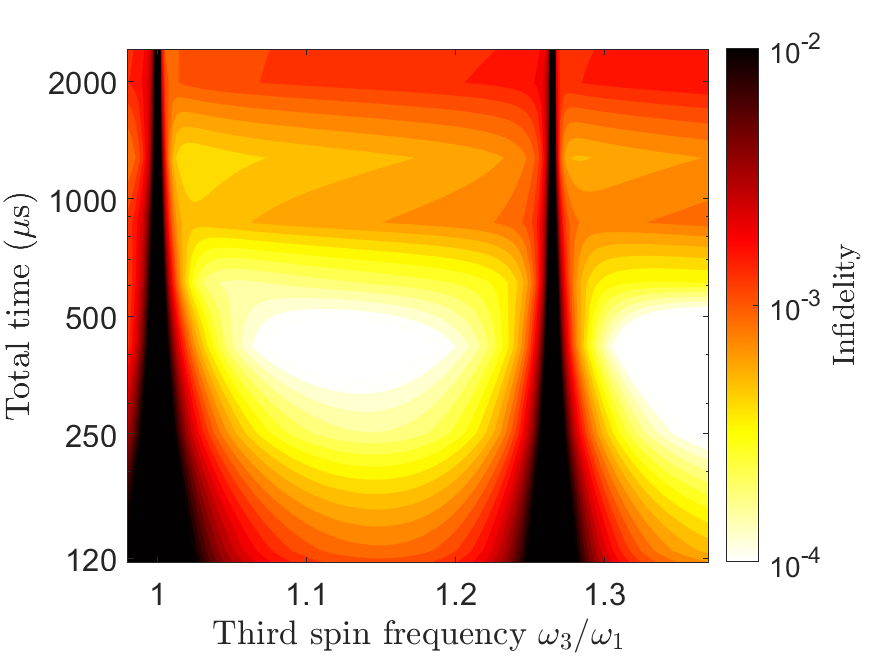
Parallel selective nuclear-spin addressing for fast high-fidelity quantum gates, B. Tratzmiller, J. F. Haase, Z. Wang, and M. B. Plenio, Phys. Rev. A 103, 012607
DOI: doi.org/10.1103/PhysRevA.103.012607
Due to their long coherence times, nuclear spins have gained considerable attention as physical qubits. Their interaction can be mediated by nitrogen vacancy (NV) centers in diamond. In this work we generalize PulsePol, a pulse sequence developed in the Institute of Theoretical Physics to achieve robust polarization transfer from NV centers to nuclear spins, to a sequence that is resonant to two frequencies simultaneously, allowing to perform gates between two nuclear spins.
This approach results in efficient entangling gates that, compared to standard techniques, reduce the gate time by more than 50% when the gate time is limited by off-resonant coupling to other spins, and by up to 22% when the gate time is limited by small electron-nuclear coupling.
Precise Spectroscopy of High-Frequency Oscillating Fields with a Single-Qubit Sensor, Y. Chu, P. Yang, M. Gong, M. Yu, B. Yu, M. B. Plenio, A. Retzker, and J. Cai, Phys. Rev. Applied 15, 014031
DOI: doi.org/10.1103/PhysRevApplied.15.014031
In recent years our group has been interested in the application of NV centers for the detection of weak classical or quasi-classical fields. In our earlier works (e.g. Schmitt et al, Science 2017) we had been interested in the detection of fields due to the precession of nuclear spins in an external magnetic field which finds application in NMR. Such fields oscillate in the MHz regime, but there is also considerable interest in the detection of fields in the GHz regime, that is microwaves. To achieve this, the pulsed schemes of our earlier works are hard to realise at sufficient rates so that we had to change the detection protocol employing continuous control fields, much in the spirit of optical heterodyne detection, that enable the comparison of the known driving field with the unknown high frequency signal field.
Contact



Ulm University
Institute of Theoretical Physics
Albert-Einstein-Allee 11
D - 89081 Ulm
Germany
Tel: +49 731 50 22911
Fax: +49 731 50 22924
Office: Building M26, room 4117
Click here if you are interested in joining the group.
Most Recent Papers
Accelerating two-dimensional electronic spectroscopy simulations with a probe qubit protocol, Phys. Rev. Research 7, 023130 (2025), arXiv:2411.16290
13C hyperpolarization with nitrogen-vacancy centers in micro- and nanodiamonds for sensitive magnetic resonance applications, Sci. Adv. 11, eadq6836 (2025), arXiv:2403.14521
YASTN: Yet another symmetric tensor networks; A Python library for Abelian symmetric tensor network calculations, SciPost Phys. Codebases (2025), arXiv:2405.12196
Unlocking Heisenberg Sensitivity with Sequential Weak Measurement Preparation, Quantum 9, 1590 (2025), arXiv:2403.05954
Time dependent Markovian master equation beyond the adiabatic limit, Quantum 8, 1534 (2024), arXiv:2304.06166
