Since the observation of the first Bose-Einstein condensates (BECs) in 1995 by Eric Cornell, Carl Wiemann and Wolfgang Ketterle BECs have become a versatile tool in the investigation of quantum phenomena. In particular, interferometers based on matter waves enable high-precision measurements of electromagnetic and gravitational fields as well as accelerations and rotations. Furthermore, they have been employed in the determination of fundamental physical constants such as the Newton constant \(G \) or the fine-structure constant \( \alpha \), and tests of Einstein's equivalence principle.
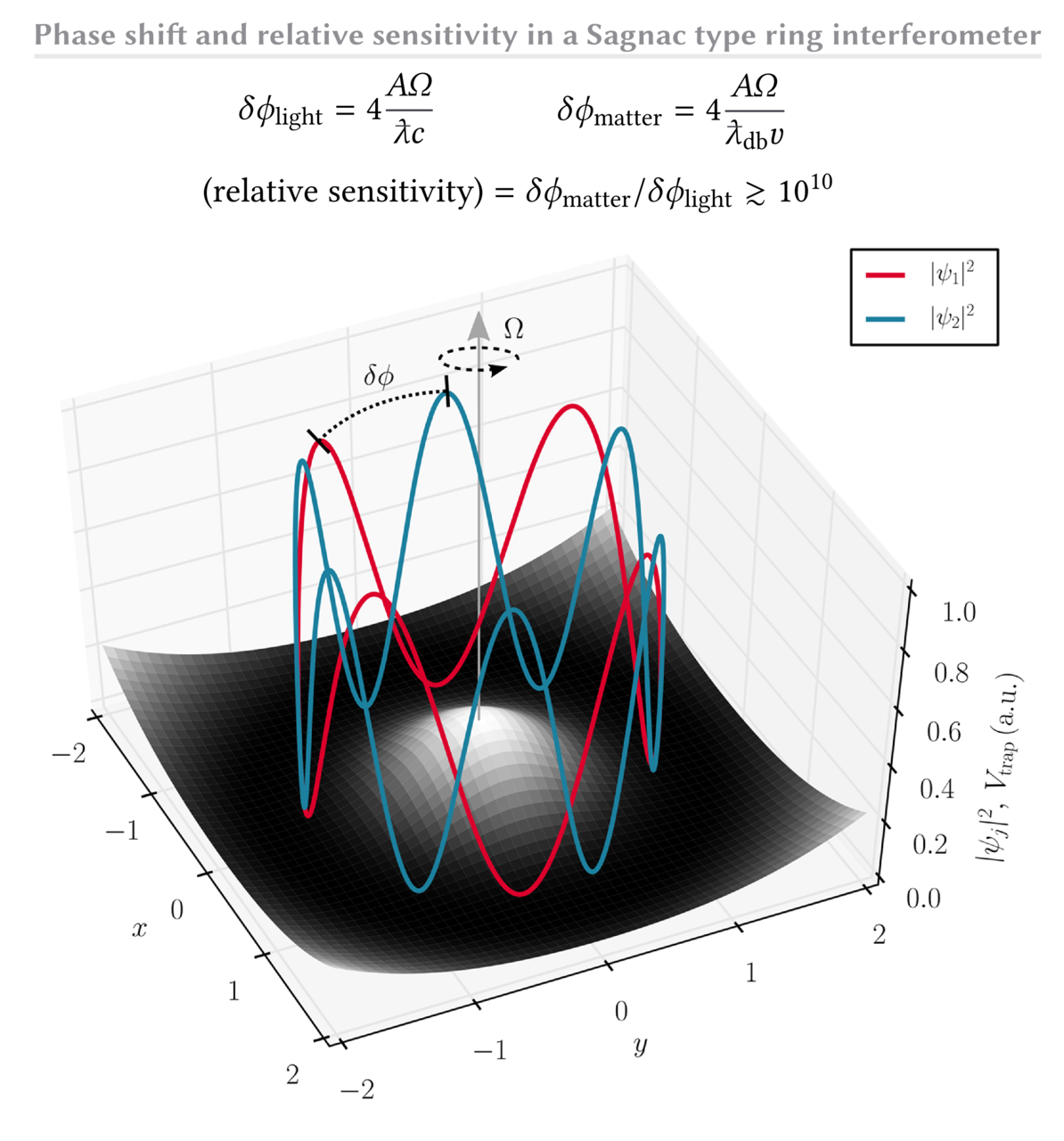
Indeed, BEC-based devices can attain much higher sensitivities than light interferometers of the same size. This advantage is due to the use of matter waves whose reduced wavelength \( \lambda_{db}/2\pi \) is much smaller than that of laser light used in a classical interferometer. Figure 1 compares and contrasts a classical Sagnac gyroscope with a matter wave based Sagnac gyroscope.
Moreover, the sensitivity of BEC interferometers depends crucially on the enclosed space-time area, that is the enclosed area \( A \) and the velocity \( v \) of the atoms. Therefore, gravity imposes a fundamental limit for experiments performed on earth due to the limited drop time available for a BEC inside a typical setup. Fortunately, ring geometries, with their inherent periodicity offer a way out of this dilemma.
Similar to a ring-laser gyroscope a BEC ring-trap interferometer allows for the precision measurement of rotations. However, the use of a BEC, described by the non-linear Gross-Pitaevskii equation, precludes a straightforward and purely analytical description of such a gyroscope. Hence, the quantum limit of such a device is yet unknown. In addition, the periodic boundary conditions of the ring trap lead, within certain parameter regimes, to a quadratic energy spectrum of the BEC, which allows one to establish a connection to Gauss sums and number theory.
In our project we investigate three aspects of a matter wave Sagnac interferometer using a combination of analytical and numerical methods: (i) non-linear dynamics of the BEC inside a ring trap, (ii) minimal rotation rate detectable with such a gyroscope in the presence of quantum fluctuations, i.e. the quantum limit of such a device, and (iii) connection to number theory due to the periodic boundary conditions and the possible application thereof to enhance the sensitivity of the gyroscope.