Contributors
J. Fischbach, M. Freyberger
Collaborations
-
Funding
-
Entanglement is a hallmark of quantum physics and a genuine quantum effect with no classical counterpart. Besides being of fundamental importance, it is used in a plethora of applications in the emerging fi eld of quantum technologies, for example in quantum networks or quantum metrology. Usually entangled states are prepared using high-precision control of very well-isolated quantum systems. In this case, the influence of the surrounding environment can be mostly neglected.
In our work, we examine an alternative approach of preparing entangled states by explicitly exploiting the interaction of the system with the environment. In this approach, we engineer the interaction of the system and the environment to some degree such that the dissipative time evolution drives the system into an entangled steady-state. Hereby we focus on bipartite systems in non-Markovian environments.
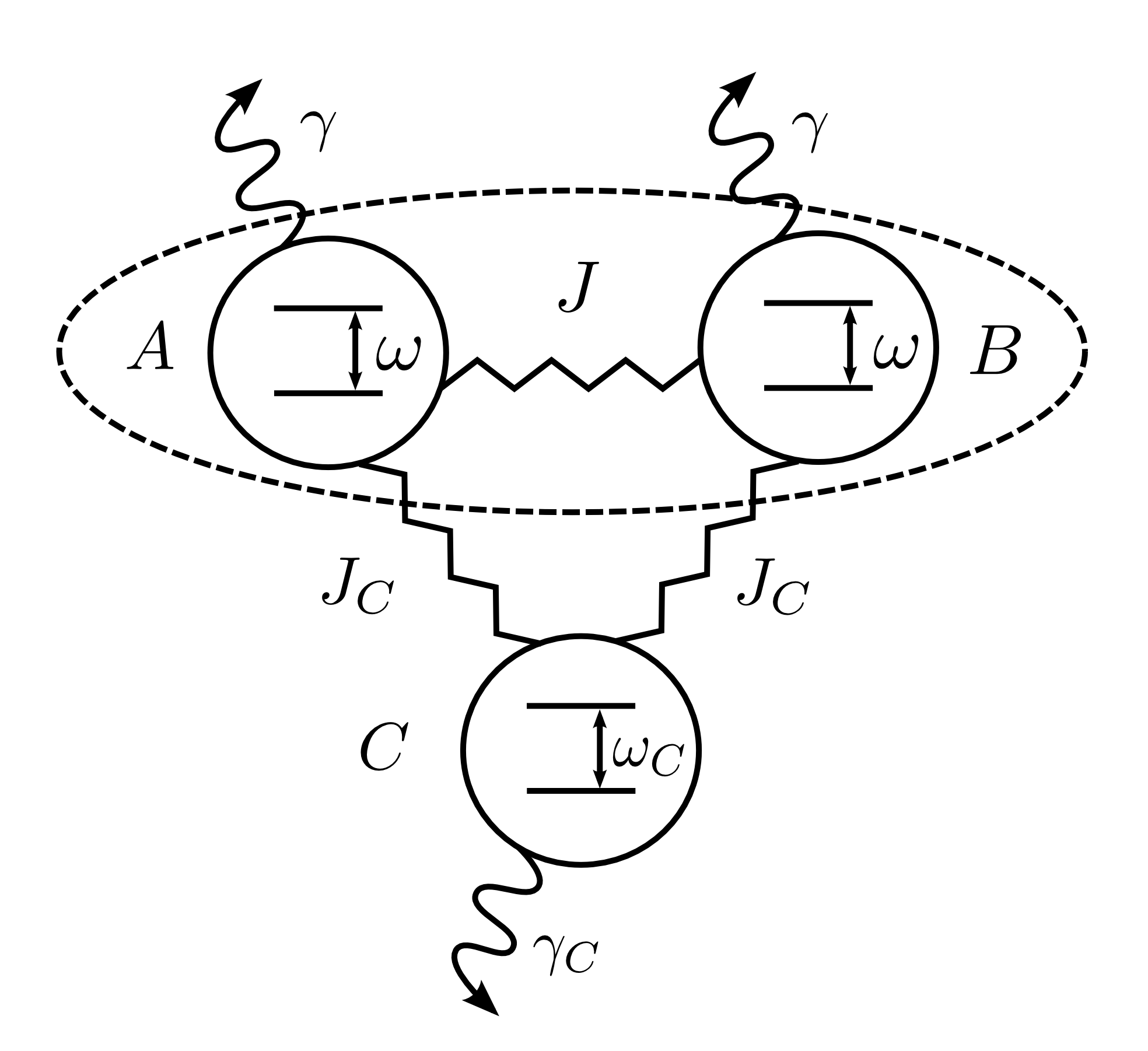
Fig. 1: Our model is composed of three coupled two-level systems \( A \), \( B\) and \(C\) and all of them are influenced by local environments, as indicated by the curly arrows. We examine the bipartite entanglement between \(A\) and \(B \) under the influence of the dissipative ancilla \(C \), which forms an engineered environment.
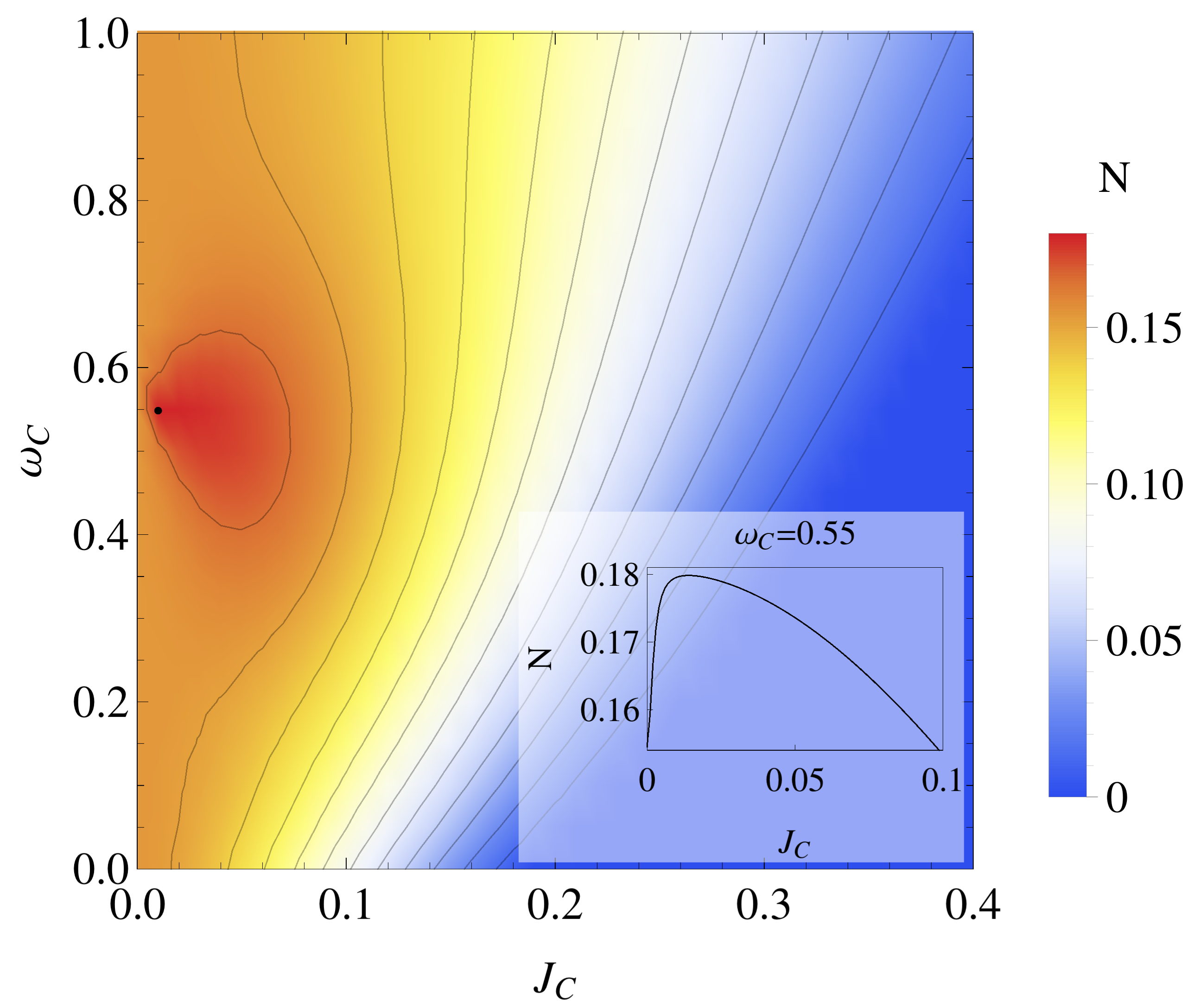
Fig. 2: The negativity \( N \) in the steady-state of the systems \( A \) and \( B \) depends on the eigenfrequency \( \omega_c \) and the coupling strength \( J_c \) of the dissipative ancilla \( C \). The black dot and the inset demonstrate that by engineering the ancilla \( C \) appropriately an enhanced steady-state entanglement can be obtained.
For example, we examine [1] two-level systems \( A \), \( B \) and an ancilla \( C \), which are coupled with each other, as indicated in Fig. 1. All three systems are subject to decoherence, as indicated by the curly arrows. The ancilla \( C \) forms a non-Markovian environment for the system \( A \) and \( B \), which we are able to engineer to some degree. By choosing the right parameters of coupling strength \( J_c \) and eigenfrequency \( \omega_c \) for the ancilla \( C \), we can increase the bipartite entanglement between \( A \) and \( B \), as measured by the negativity \( N \) and shown in Fig. 2.
Beyond this setup, which realizes a simple, non-Markovian environment, we also examine other bipartite systems that interact with intricate non-Markovian environments. Using such systems for the dissipative preparation of entangled states constitutes an alternative approach to conventional preparation schemes.
J. Fischbach, M. Freyberger
-
-
[1] J. Fischbach and M. Freyberger, Steady-state entanglement enhanced by a dissipative ancilla, Phys. Rev. A 92, 052327 (2015)