Contributors
C. Tempel, W.P. Schleich
Collaborations
M.O. Scully (Texas A&M University, College Station, USA)
Funding
Texas A&M University Institute for Advanced Study (TIAS)
The prevalent interpretation of quantum mechanics, now commonly termed Copenhagen interpretation, is predominantly utilised in research as well as teaching. However, several alternative interpretations exist, such as the Everett many-worlds theory, the statistical interpretation, consistent histories, the de-Broglie-Bohm theory and many more. The last named variant in particular is an ontological theory, i.e. it purposely retains objects that are empirically unobservable, in turn allowing for an interpretation of measurement results. In this particular case, the wave function in position representation is supplemented by the assumption that the particles have definite configurations at all times. The motion of these configurations is then governed by a guidance equation related to the wave function. As a result, this interpretation can be characterised as a non-local hidden-variable theory.
The connection of path-lines traversed by Bohm particles and the hydrodynamical approach is well known. In certain cases, a further association may be made to quantiles, yielding a one-to-one relation of the guidance equation to this tool originating in classical probability theory. This relation fails in higher dimensional cases exhibiting dynamics that form correlations of the relevant variables, resulting in quantiles not being applicable anymore. We explore possible extensions of this approach, in particular in the context of copula theory.
Further, we explore the extension of the relevant mathematical methods to continuous Hilbert spaces other than position space as well as discrete varieties thereof. Relevant to the topic is in particular the amount of eigenstates involved. As for the former case of a representation exhibiting a continuous spectrum, Fig. 1 illustrates the evolution of path-lines in one-dimensional momentum space for the example of a particle in a box.
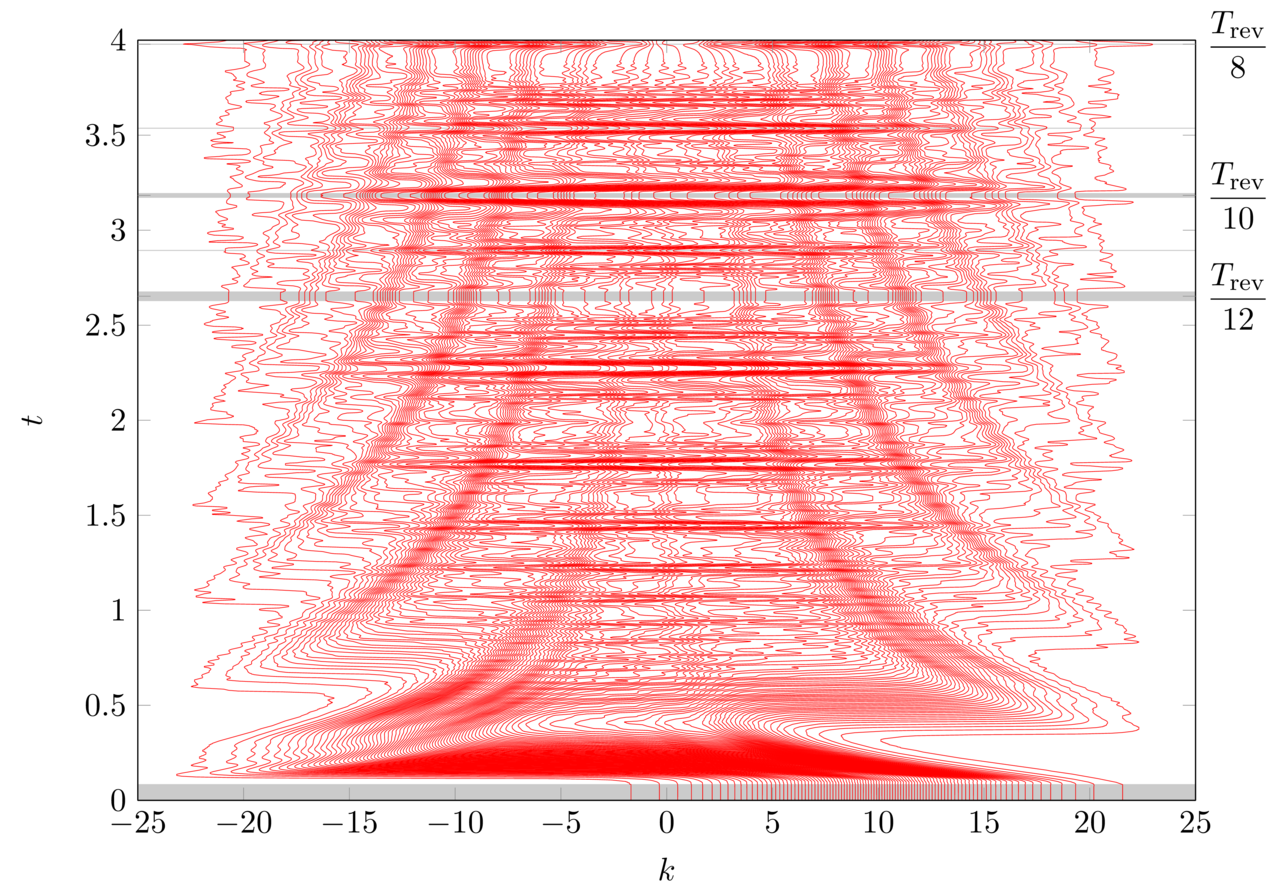
Fig. 1: Momentum space path-lines corresponding to a particle in a one-dimensional infinitely deep square well. They correspond to a Gaussian wave packet with a non-vanishing initial momentum. While the motion of the packet is rather complex, similar to that in position space, revivals lead to free evolution while the packet is not interacting with the walls. Grey areas highlight these time spans.
C. Tempel, W.P. Schleich
M.O. Scully (Texas A&M University, College Station, USA)
Texas A&M University Institute for Advanced Study (TIAS)
[1] W.P. Schleich, M. Freyberger, and M.S. Zubairy, Reconstruction of Bohm trajectories and wave functions from interferometric measurements, Phys. Rev. A 87, 014102 (2013)