Institute of Quantum Physics

Quantum Free-Electron Laser

A free-electron laser (FEL), shown in Fig. 1, is the prime example of a 'Classical Laser' [1], that is we do not need quantum mechanics to understand its operation. However, there also exists a regime of the FEL dynamics, the so-called Quantum FEL [2], where quantum mechanics is indeed important. In order to investigate the emergence and the properties of this limit of FEL operation, a collaboration of the Helmholtz-Zentrum Dresden-Rossendorf e. V. and the Institute of Quantum Physics was established.

The recoil due to the scattering of the electron by the photons of the wiggler and the laser field is the relevant quantity which determines the transition from classical to quantum (see Fig. 2) in the FEL [3]. Since the recoil depends linearly on the Planck constant \( \hbar \) we obtain the deep quantum limit when the recoil is the dominating momentum scale. In this regime we can describe the electron dynamics as an effective two-level system.

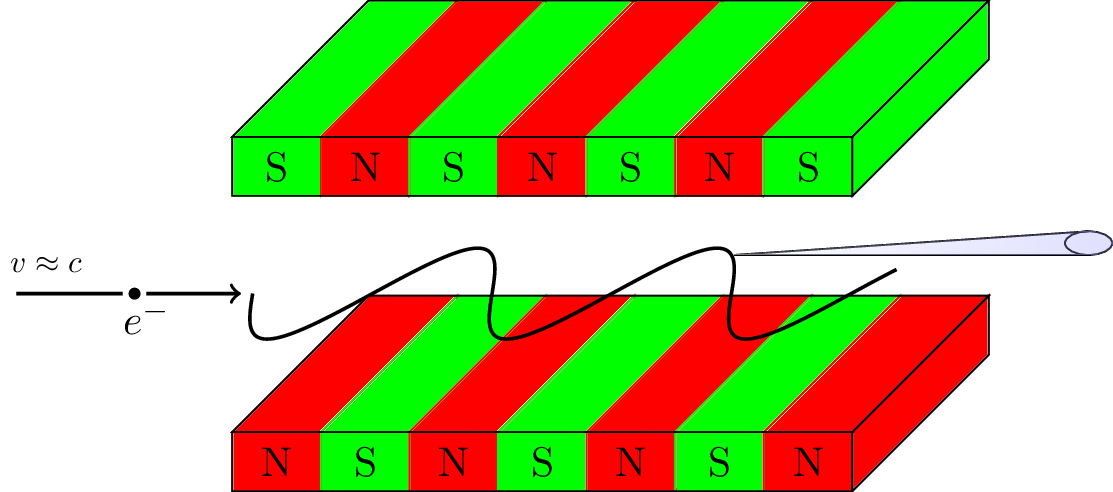
Fig. 1: Basic scheme of a FEL: Electrons travel with velocities close to the speed of light through an alternating array of magnets, called 'wiggler'. Due to the Lorentz force the electrons oscillate and emit radiation.

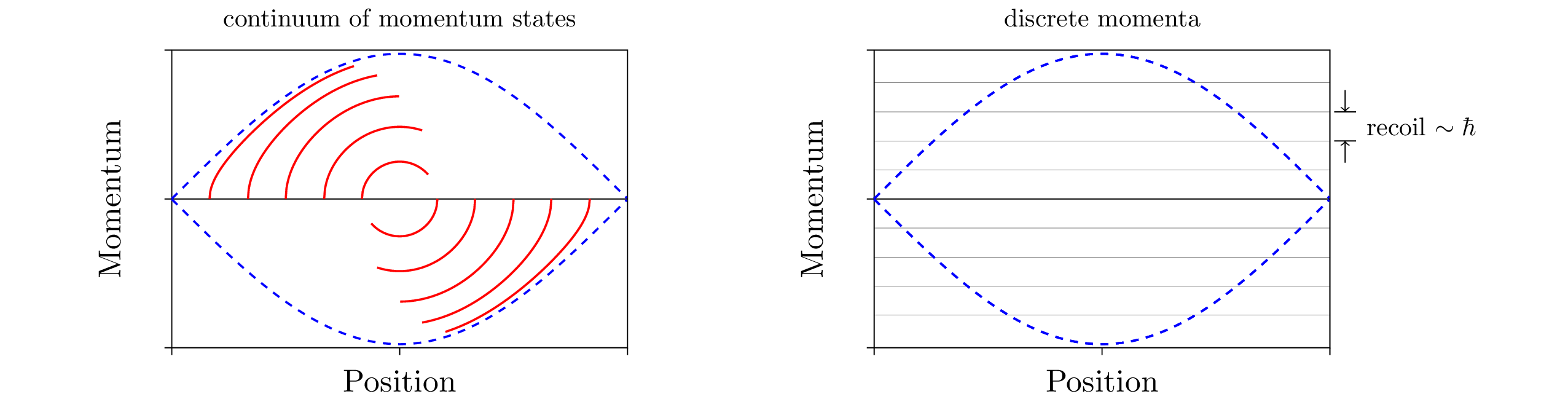
Fig. 2: FEL dynamics in phase space: the classical case (left) with continuous trajectories, vs. the quantum regime (right) with discrete momenta separated by the recoil.

We study the radiation of a Quantum FEL, e. g. the photon statistics or the linewidth. Moreover, we (i) develop a collective approach, where many electrons interact simultaneously with the radiation, and (ii) include the interaction with many modes of the electromagnetic field. Both extensions to our model are necessary to go to the Self-Amplified Spontaneous Emission (SASE) mode of operation and eventually achieve an X-ray Quantum FEL.

References

[1] M. Borenstein and W. E. Lamb, Classical Laser, Phys. Rev. A 5, 1298 (1972).
[2] R. Bonifacio, N. Piovella and G. R. M. Robb, The quantum free electron laser: A new source of coherent, short-wavelength radiation, Fortschr. Phys. 57, 1041 (2009).
[3] P. Kling, E. Giese, R. Endrich, P. Preiss, R. Sauerbrey and W. P. Schleich, What defines the quantum regime of the free-electron laser?, New J. Phys. 17, 123019 (2015).
[4] P. Kling, R. Sauerbrey, P. Preiss, E. Giese, R. Endrich und W. P. Schleich, Quantum regime of a free-electron laser: relativistic approach (submitted to Appl. Phys. B, 2016)