Institut für Quantenphysik

Fractional Josephson Vortices

Within the SFB/TRR-21 (control of quantum correlations in tailored matter) we study fractional Josephson vortices in long Josephson junctions. These vortices carry a fraction of the magnetic flux quantum and are pinned at phase discontinuities (fabricated in a controlled way) of the Josephson junction. In the simplest case they carry one half of a flux quantum (“semifluxons”) and are similar to spin 1/2 systems with degenerate energies of “up” and “down” states separated by an energy barrier. The goal of the SFB project is to demonstrate that the quantum limit of such systems, where quantum tunneling between the “up” and states “down” through the energy barrier becomes important, can be reached. In close collaboration with the experimental group of Reinhold Kleiner (Tübingen) we develop a quantum mechanical description of such systems and estimate parameters for which the quantum nature of fractional Josephson vortices can be observed.

The dynamics of the Josephson phase of fractional vortices can be described by a modified sine-Gordon equation which takes into account phase discontinuities in the Josephson junction. It turned out that collective coordinates which map the dynamics of the Josephson phase of the full system to the motion of a single particle in an effective 1D potential are useful to investigate quantum properties of one or two fractional Josephson vortices. The limiting case of a point-like Josephson junction corresponds to a particle in a washboard potential. We have studied two typical tunneling problems: quantum tunneling (coherent oscillations) between two degenerate states in a double-well potential and quantum escape from a metastable potential. According to our estimates the quantum limit of long Josephson junctions can be reached with present technology, that is at temperatures not lower than 20-30 mK.

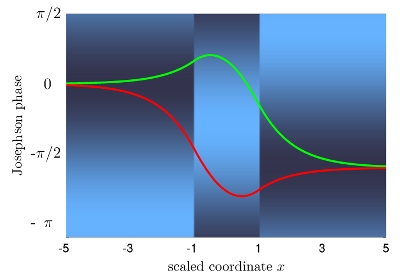
Fig. 1: Potential energy density and Josephson phase in a long Josephson junction with two phase discontinuities at \( x=\pm1\). Light colors indicate high potential energy whereas dark colors indicate low potential energy. The two Josephson phases drawn in red and green have minimal energy and are separated by an energy barrier. In the quantum limit, quantum tunneling between the two phases becomes important.

"Quantum" escape from a resonantly driven metastable potential has two interpretations. In the language of quantum mechanics, a resonant driving field brings the particle in to an excited state from where it can tunnel much simpler. In the language of classical physics a resonant driving field excites oscillations with large amplitudes and the particle finally escapes. It is still an open question how to interpret experimental data. Therefore, we look for criteria that allow us to distinguish these two processes.

References

[1] M. Grupp, W. P. Schleich, E. Goldobin, D. Koelle, R. Kleiner, and R. Walser, Emergence of atomic semifluxons in optical Josephson junctions, Phys. Rev. A 87, 021602 (2013).
[2] D. M. Heim, W. P. Schleich, P. M. Alsing, J. P. Dahl, and S. Varro, Tunneling of an energy eigenstate through a parabolic barrier viewed from Wigner phase space, Phys. Lett. A 377, 1822 (2013).
[3] D. M. Heim, N. G. Pugach, M. Y. Kupriyanov, E. Goldobin, D. Koelle, and R. Kleiner, Ferromagnetic planar Josephson junction with transparent interfaces: a φ junction proposal, J. Phys.: Condens. Matter 25, 239601 (2013).