Contributors
F. Di Pumpo, H. Weber, M. Freyberger
Collaborations
-
Funding
-
A widely used method in metrology is the time-of-flight measurement. The momentum can be determined via the measurement of a time difference if fixed positions are given. Figure 1 shows such a concept.

Fig. 1: The scheme illustrates the classical time-of-flight momentum measurement. The momentum of a particle is calculated via the measurement of the times which are measured at fixed positions.
In this work, we examine quantum mechanical time-of-flight momentum measurements, which are motivated by the classical time-of-flight concept. Our setup is modeled by a Hamiltonian for a free particle interacting with two quantum pointers, see Ref. [1-4], which are able to record information about the particle.
For this model we can solve the corresponding three-particle dynamics in the Heisenberg picture and use this solutions in order to define an operational momentum operator and an operational momentum eigenvalue, both in the spirit of classical time-of-flight measurements. This allows us to examine two fundamental aspects: First, we verify that the expectation value of the operational momentum operator equals the one of the original momentum operator describing the single-particle system. Moreover, we examine the momentum variance and characterize additional noise caused by the interaction of the particle with the pointers. This additional noise is then minimized by preparing appropriate pointer states, shown in Fig. 2.
Second, we analyze in what sense position measurements on the pointers reduce the conditional quantum state of the particle and hence define its momentum. All results can be found in Ref. [5].
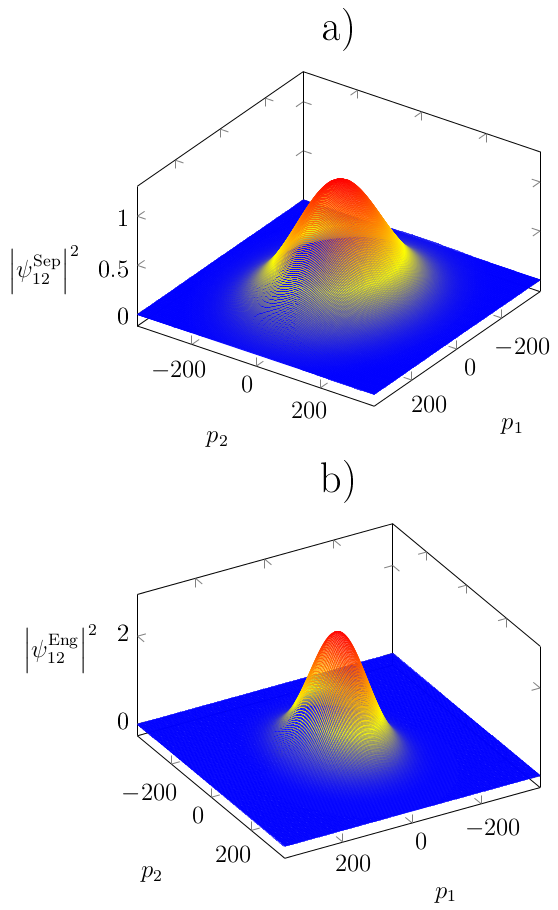
Fig. 2: For the optimized pointer states we obtain in the separable case a) as well as in the entangled case b) a Gaussian. Both states are squeezed and the entangled probability density is more located in the momentum space as in the separable case.
F. Di Pumpo, H. Weber, M. Freyberger
-
-
[1] E. Arthurs and J. L. Kelly, On the simultaneous measurement of a pair of conjugate observables, Bell Labs Tech. J. 44, 725–729 (1965)
[2] S. Stenholm, Simultaneous measurement of conjugate variables, Ann. Phys. 218, 233-254 (1992)
[3] M. Bußhardt and M. Freyberger, Timing in quantum measurements of position and momentum, Phys. Rev. A 82, 042117 (2010)
[4] M. Bußhardt and M. Freyberger, Energy and time in simultaneous measurements of position and momentum, Europhys. Lett. 96, 40006 (2011)
[5] F. Di Pumpo, Operational observables in quantum mechanics, Masterarbeit Physik, Institut für Quantenphysik, Universität Ulm (2017)