Wie muss man eine Murmelbahn bauen, damit die Murmel am schnellsten hinunterrollt ? 

Wie findet man die kürzeste Verbindung zwischen zwei Punkten, die dazu noch an einem Hindernis vorbeiführt ? 

Warum sind Seifenblasen rund ? 

Diese Fragen und viele mehr lassen sich mithilfe der Variationsrechnung beantworten. 

Grundsätzlich haben alle diese Probleme eines gemeinsam: Sie verlangen uns die Minimierung oder Maximierung einer "Funktion von Funktionen", sogenannten Funktionalen, ab. Solche Probleme hängen von mehr als nur endlich vielen Parametern ab, was uns bereits in das tiefe Kapitel der unendlichdimensionalen Analysis befördert. 

Angefangen im frühen 18. Jahrhundert mit Beiträgen von Leonhard Euler, Sir Isaac Newton und Joseph-Louis Lagrange hat sich die Variationsrechnung Hand in Hand mit zahlreichen anderen Disziplinen entwickelt: 

• Physik. Trajektorien zu finden, die Energien minimieren sind nicht erst seit Newtons "Principia" ein erklärtes Ziel der Physik. Das Mitte des 18.Jh von Hamilton gefundene Prinzip der kleinsten Wirkung lässt sich als eine vollkommen variationelle Formulierung der Mechanik sehen.
• Geometrie. Die Frage nach der kürzesten Verbindung zweier Punkte mag im euklidischen Anschauungsraum einfach erscheinen, wie aber findet man einen kürzesten Weg, wenn man sich nur auf der Oberfläche eines Donuts oder eines anderen gekrümmten Objektes bewegen darf? 
• Funktionalanalysis.  Die Funktionalanalysis liefert einen großen Pool an Werkzeugen, mit denen sich nicht nur lineare Funktionale untersuchen lassen. Die Variationsrechnung bedient sich dieser Methoden und hat auch einige neue funktionalanalytische Methoden inspiriert. 
• Differentialgleichungen. Unter Bedingungen, die wir im Kurs diskutieren werden, erfüllen Extrema eines Funktionals eine (partielle) Differentialgleichung, die sogenannte Euler-Lagrange-Gleichung. Damit lässt sich die Frage nach einem Extremum eines Funktionals in eine Frage nach einer Lösung einer Differentialgleichung übersetzen. Dieser Übergang ist - in beide Richtungen - von höchster mathematischer Relevanz. 
• Numerik.  Einige numerische Fragestellungen beruhen auf Variationsproblemen, so zum Bespiel ist die Variationsrechnung ein nicht wegzudenkendes Werkzeug in der Kontrolltheorie. An der Schnittstelle bildete sich in den 1950er Jahren die Theorie der optimalen Steuerungen, die der Mathematik bis heute wichtige Konzepte beschert.

Das obere Bild zeigt Costas Minimalfläche, die Form eines Seifenfilms, der entsteht, wenn man die drei silbernen Ringe in der gezeigten Anordnung in Seife taucht. 

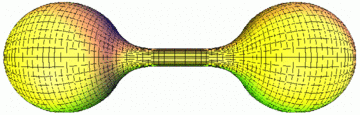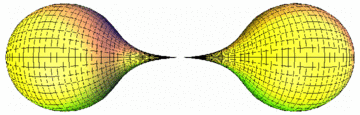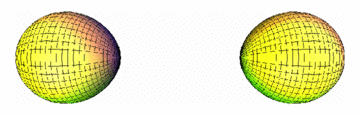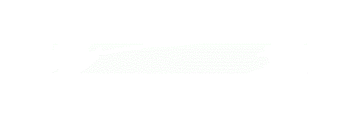
Das untere Bild zeigt, wie sich eine Fläche unter dem mittleren Krümmungsfluss verhält. Dieser ist ein Beispiel für einen sogenannten Gradientenfluss, den man in manchen Fällen benutzen kann, um kritische Punkte von Funktionalen zu approximieren.