Seminar: Spatial stochastic modeling, supported by methods of machine learning
The quantitative analysis of digital (image) data is an important tool in various scientific disciplines such as medicine, geography, weather forecast or materials science. Mathematical techniques for pattern recognition or for the description of complex image structures with the help of spatial stochastic models can make valuable contributions. Stochastic geometry provides a wide range of spatial stochastic models for various applications, e.g., point processes to describe point patterns in space, random graphs for modeling complex network structures and random tessellations for describing mosaics (cellular or granular structures). In order to spatially model such structures which are often present in the form of image data, initial processing steps are often necessary to extract the necessary information from images, e.g., extraction of points, detection of boundaries. Recently, methods from machine learning emerged as useful tool for image processing and, thus, for spatial stochastic modeling. For example, convolutional neural networks can be utilized to enhance the image processing procedure which is often a necessary step prior to modeling. Moreover, methods of machine learning are used for predicting physical properties like, for example, the conductivity of spatial stochastic models which are otherwise difficult to compute. On the other hand, machine learning methods can benefit from spatial stochastic models by generating artificial training data.
In this seminar, therefore, not only basic mathematical models for the description of image data are introduced (random closed sets, point processes, tessellation models) but also methods of machine learning are dealt with. In addition, various scientific studies which utilize the presented methods are discussed.
The seminar can be used as a suitable preparation for writing a Bachelor or Master thesis on similar topics.
| prerequisites: | WR |
| target audience: | Bachelor and Master students in "Wirtschaftsmathematik", "Mathematik", "Mathematische Biometrie", "CSE" or "Lehramt Mathematik" |
| credits: | 4 |
| number of places: | 8 |
| schedule: | May 31, June 7, June 14, June 21 |
| time: | 2-4 pm |
| enrolment: | via mail to Orkun Furat |
Contact
Seminar Supervisor
Prof. Dr. Volker Schmidt
E-Mail: volker.schmidt@uni-ulm.de
Seminar Advisor
Orkun Furat
E-Mail: orkun.furat@uni-ulm.de
Preliminary list of seminar talks
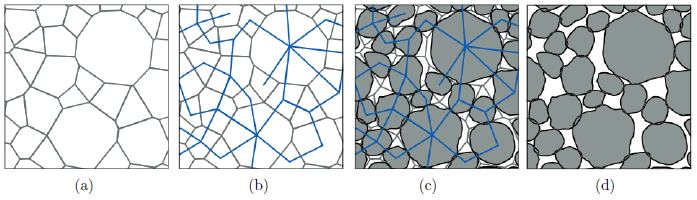
1. Stochastic geometry: point processes, Boolean models and random tessellations
| Speaker: | Thomas Wilhelm |
| Date: | May 31 |
In this talk some basic models from stochastic geometry are presented [1]. Special focus will lie on the Poisson process which is the basis for more advanced point processes for modeling random point patterns. Then, based on point processes, more advanced models are introduced, like, for example random tessellations, the realizations of which are partitions of space. Tessellation models are used for modeling, for exampl, cellular or granular structures.
[1] S.N. Chiu, D. Stoyan, W.S. Kendall, J. Mecke. Stochastic Geometry and its Applications. J. Wiley & Sons (2013).
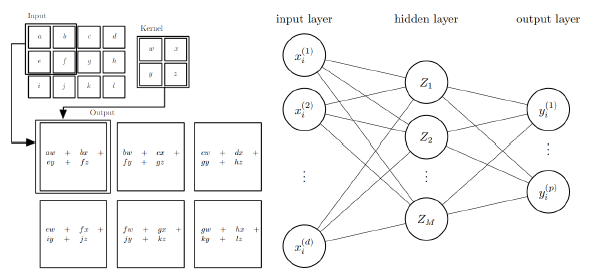
2. Machine learning: supervised learning with (convolutional) neural networks
| Speaker: | Joachim Hegenauer |
| Date: | May 31 |
Methods of machine learning provide useful tools for the processing of image data, for example in image classification and segmentation tasks [2]. While conventional image processing techniques rely on carefully calibrated algorithms for their decision making process, machine learning techniques like convolutional neural networks bypass this issue. Since these neural networks can be considered to be regression models, which are fitted (trained) by choosing appropriate regression parameters, they require for the training procedure pairs of input and target (ground truth) values.
[2] I. Goodfellow, Y. Bengio, A. Courville, Y. Bengio. Deep Learning. Cambridge: MIT press (2016).
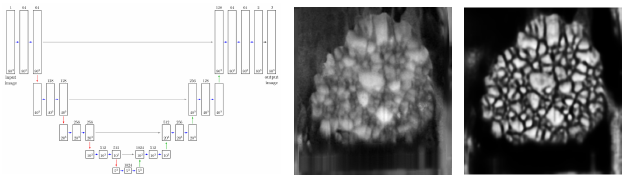
3. Segmentation of tomographic image data using the U-Net architecture
| Speaker: | Tim Remiger |
| Date: | June 7 |
In order to spatially model structures depicted in image data, initial processing steps are often necessary to extract the necessary information for spatial modeling. Recently, a specific neural network, namely the U-Net, has become a rather popular tool for image segmentation in numerous scientific fields [3]. In this talk, the application of the U-Net architecture on tomographic image data of polycrystalline materials (e.g., alloys or metal oxides used in batteries) is given. Furthermore, techniques like, for example, data augmentation and the modification of loss functions, are presented to decrease the amount of data necessary for training, or to even deal with partially labeled ground truth data [4].
[3] O. Ronneberger, P. Fischer, T. Brox. U-net: Convolutional networks for biomedical image segmentation. In International Conference on Medical image computing and computer-assisted intervention (2015). Springer, pp. 234-241
[4] O. Furat, D. Finegan, D. Diercks, F. Usseglio-Viretta, K. Smith and V. Schmidt, Mapping the architecture of single electrode particles in 3D, using electron backscatter diffraction and machine learning segmentation. Journal of Power Sources 483 (2021), 229148.
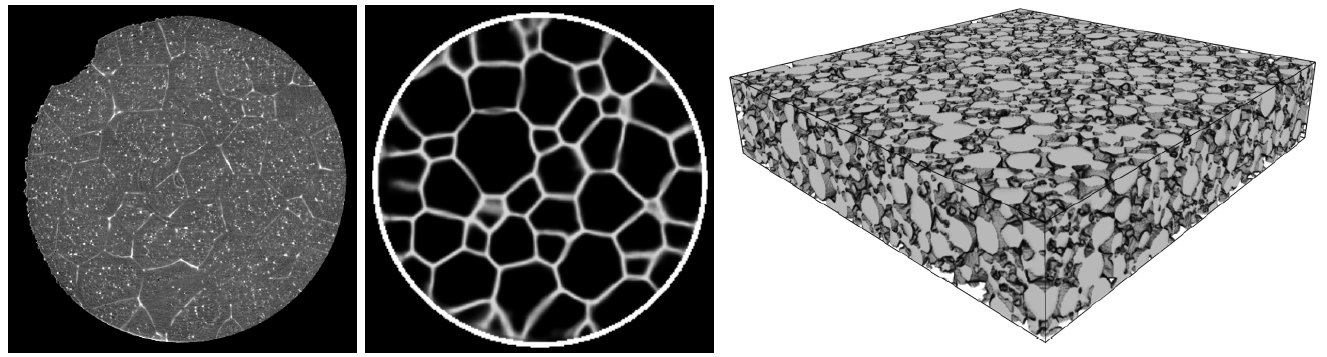
4. Predicting microstructure-property relationships, using data-driven stochastic geometry modeling and statistical learning
| Speaker: | Tom Kirstein |
| Date: | June 7 |
The microstructure of advanced functional materials (e.g., electrodes in solid oxide fuel cells or batteries) significantly influences the physical properties (e.g. conductivity) of the material [5]. Imaging techniques, like electron microscopy (EM), can provide 3D image data of a material's micostructure. However, imaging a large amount of materials for investigating microstructure-property relationships is both costly and time-consuming. This issue can be remedied by using stochastic geometry models for generating a large variety of virtual, but realistic microstructures, the physical properties of which can be determined via numerical simulations (e.g. finite element method) [6]. This approach provides a large database for investigating microstructure-property relationships with methods from machine learning [5, 7].
[5] M. Neumann, O. Stenzel, F. Willot, L. Holzer and V. Schmidt, Quantifying the influence of microstructure on effective conductivity and permeability: virtual materials testing. International Journal of Solids and Structures 184 (2020), 211-220.
[6] O. Stenzel, H. Hassfeld, R. Thiedmann, L.J.A. Koster, S.D. Oosterhout, S.S. van Bavel, M.M. Wienk, J. Loos, R.A.J. Janssen and V. Schmidt, Spatial modelling of the 3D morphology of hybrid polymer-ZnO solar cells, based on electron tomography data. Annals of Applied Statistics 5 (2011), 1920-1947.
[7] O. Stenzel, M. Neumann, O. Pecho, L. Holzer and V. Schmidt, Big Data for microstructure-property relationships: A case study of predicting effective conductivities. AIChE Journal 63 (2017), 4224–4232.
5. Stochastic microstructure modeling, using Markov random fields
| Speaker: | Niklas Eiermann |
| Date: | June 14 |
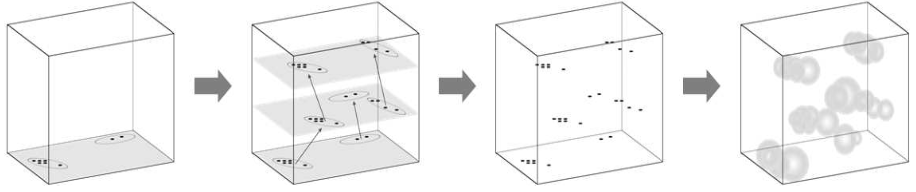
Markov random fields (MRFs) are graph models, the vertices of which are random variables. The dependency structure of these random variables is tractable by the Markov property. By chosing a regular grid as the underlying graph, the realizations of the MRF can be considered to be images, i.e., MRFs can be used as random image models. Thus, have a broad range of applications ranging from image and texture synthesis, image compression and restoration, image segmentation and super-resolution to information retrieval [8]. Especially, using MRFs for image and texture synthesis makes them interesting as stochastic geometry models. In this talk basic properties of MRFs are given and an application for generating synthetic image data of polycrystalline materials is shown [9].
[8] L.Y. Wei, S. Lefebvre, V. Kwatra, G. Turk. State of the art in example-based texture synthesis. In Eurographics 2009, State of the Art Report, EG-STAR. Eurographics Association (2009), pp. 93-117.
[9] A. Kumar, L. Nguyen, M. DeGraef, V.Sundararaghavan, V. A Markov random field approach for microstructure synthesis. Modelling and Simulation in Materials Science and Engineering (2016), 24(3), 035015.
6. Generative adversarial networks for the generation of multiphase microstructural data
| Speaker: | Andre Köhler |
| Date: | June 14 |
Generative adversial networks (GANs) which are usually models for unsupervised learning have, for example, various applications in texture and image synthesis [10]. After training with a given data set of images, these networks can generate new images which are statistically similar to those of the training data set. Therefore, GANs can be considered to be spatial stochastic models. For example, in [11] a GAN was trained with with 3D image data depicting the three-phased microstructure of lithium-ion battery cathodes and solid oxide fuell cell anodes. Then, similar to a stochastic geometry model, the trained network is able to generate virtual, but realistic 3D image data.
[10] I.J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio. Generative adversarial networks (2014). arXiv preprint arXiv:1406.2661.
[11] A. Gayon-Lombardo, L. Mosser, N.P. Brandon, S.J. Cooper. Pores for thought: generative adversarial networks for stochastic reconstruction of 3D multi-phase electrode microstructures with periodic boundaries. npj Computational Materials (2020), 6(1), 1-11.
7. Using stochastic geometry models for generating artificial training data
| Speaker: | Antonio Alves |
| Date: | June 21 |
In order to train a supervised neural network labeled training data is necessary, i.e., we require pairs of input and target output (ground truth) arguments. However, in many cases ground truth data is difficult to obtain, for example, by manual labeling or by expensive reference measurements. For many applications, this issue can by remedied by stochastic geometry modeling. For example, in image classification or segmentation tasks, in which individual objects are to be extracted by some machine learning algorithm, it is possible to generate artificial image data using a stochastic model for which the positions of the to be extracted objects are already known [12]. This approach allows for the generation of huge amounts of training data [13].
[12] J. Feinauer, T. Brereton, A. Spettl, M. Weber, I. Manke and V. Schmidt, Stochastic 3D modeling of the microstructure of lithium-ion battery anodes via Gaussian random fields on the sphere. Computational Materials Science 109 (2015), 137-146.
[13] L. Petrich, D. Westhoff, J. Feinauer, D. Finegan, S. Daemi, P. Shearing and V. Schmidt, Crack detection in lithium-ion cells using machine learning. Computational Materials Science 136 (2017), 297-305.
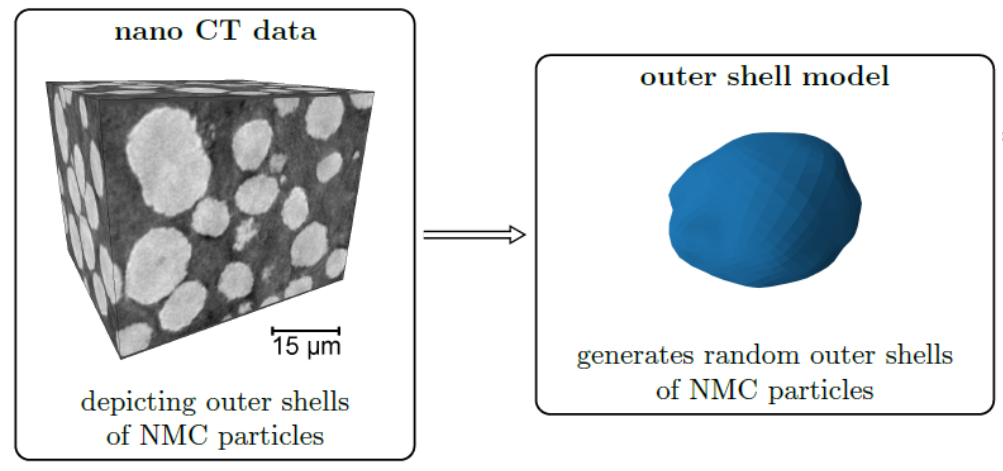
8. Generation of representative single Li-ion outer particle shells, using mixed Gaussian random fields on the unit sphere
| Speaker: | Marten Ademmer |
| Date: | June 21 |
Stochastic geometry models for the outer shell of individual particles are the basis for more complex models which consider the spatial positions of particles for the generation of virtual cathode microstructures [13]. For modeling the shape of the outer shells of such particles often random fields on the unit sphere are used. In the Gaussian case the parameters of these models can be estimated using analytical formulas [14], however, for more complex models (e.g, mixtures of Gaussian random fields) a direct estimation of model parameters is difficult. In this case machine learning libraries can be utilized for a fast optimization of model parameters [15].
[13] B. Prifling, D. Westhoff, D. Schmidt, H. Markötter, I. Manke, V. Knoblauch and V. Schmidt, Parametric microstructure modeling of compressed cathode materials for Li-ion batteries. Computational Materials Science 169 (2019), 109083.
[14] J. Feinauer, T. Brereton, A. Spettl, M. Weber, I. Manke and V. Schmidt, Stochastic 3D modeling of the microstructure of lithium-ion battery anodes via Gaussian random fields on the sphere. Computational Materials Science 109 (2015), 137-146.
[15] O. Furat, L. Petrich, D. Finegan, D. Diercks, F. Usseglio-Viretta, K. Smith and V. Schmidt, Artificial generation of representative single Li-ion electrode particle architectures from microscopy data. npj Computational Materials (accepted).