Seminar: Multivariate stochastic modeling: Classical approaches and methods of machine learning
The quantitative analysis of digital (image) data is an important tool in various scientific disciplines such as medicine, geography, weather forecast or materials science. Mathematical techniques for pattern recognition or for the description of complex image structures with the help of spatial stochastic models can make valuable contributions. Stochastic geometry provides a wide range of spatial stochastic models for various applications, e.g., point processes to describe point patterns in space, random graphs for modeling complex network structures and random tessellations for describing mosaics (cellular or granular structures). In order to spatially model such structures which are often present in the form of image data, initial processing steps are often necessary to extract the necessary information from images, e.g., extraction of points, detection of boundaries. Recently, methods from machine learning emerged as useful tool for image processing and, thus, for spatial stochastic modeling. For example, convolutional neural networks can be utilized to enhance the image processing procedure which is often a necessary step prior to modeling. Moreover, methods of machine learning are used for predicting physical properties like, for example, the conductivity of spatial stochastic models which are otherwise difficult to compute. On the other hand, machine learning methods can benefit from spatial stochastic models by generating artificial training data.
In this seminar, therefore, not only basic mathematical models for the description of image data are introduced (random closed sets, point processes, tessellation models) but also methods of machine learning are dealt with. In addition, various scientific studies which utilize the presented methods are discussed.
The seminar can be used as a suitable preparation for writing a Bachelor or Master thesis on similar topics.
| prerequisites: | Introduction to Probability Calculus |
| target audience: | Bachelor and Master students in "Wirtschaftsmathematik", "Mathematik", "Mathematische Biometrie", "CSE" or "Lehramt Mathematik" |
| credits: | 4 |
| time and location: | Tuesday 16:15-18:15; Room 220, Helmholtzstraße 18. Alternative date for 06.06.: Wednesday, 07.06., 16:00-18:00; Room E20, |
| enrolment: | via mail to Phillip Gräfensteiner |
Contact
Seminar Supervisor
Prof. Dr. Volker Schmidt
E-Mail: volker.schmidt@uni-ulm.de
Dr. Matthias Neumann
E-Mail: matthias.neumann@uni-ulm.de
Dr. Orkun Furat
E-Mail: orkun.furat@uni-ulm.de
Seminar Advisor
Phillip Gräfensteiner
E-Mail: phillip.graefensteiner@uni-ulm.de
List of seminar talks
The morphology of nanoporous glass: stochastic 3D modeling, stereology and the influence of pore width
| Speaker: | Phillip Gräfensteiner |
| Date: | 18.04.2023 |
Using super-resolution for the characterization of operating conditions on particle cracking in Li-ion battery cathodes
| Speaker: | Dr. Orkun Furat |
| Date: | 18.04.2023 |
Stochastic 3D modeling of nanostructures in battery materials based on FIB/SEM data
| Speaker: | Dr. Matthias Neumann |
| Date: | 24.04.2023 |
Stochastic microstructure modeling of twinned polycrystals
| Speaker: | Philipp Rieder |
| Date: | 24.04.2023 |
Continuous representation of voxelized image data for polycrystaline microstructures using 3D warped tessellation
| Speaker: | Thomas Wilhelm |
| Date: | 02.05.2023 |
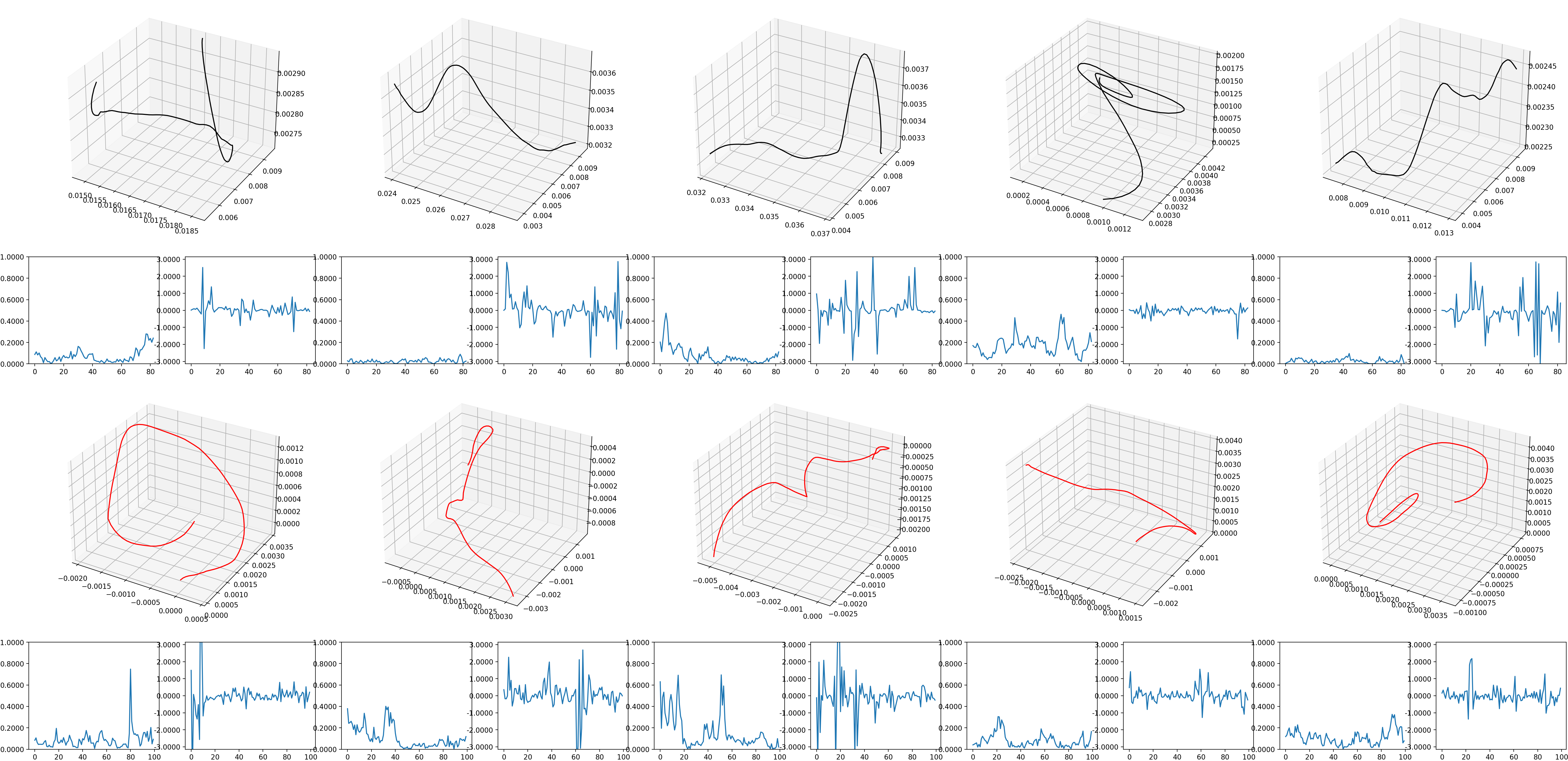
Multidimensional characterization of particle morphology and mineralogical composition using CT data and R-vine copulas, with applications to quantitative assessment of separation quality
| Speaker: | Tom Kirstein |
| Date: | 02.05.2023 |
Quantitative characterization of hydrophobic agglomeration for different stirrer designs using multivariate time-dependent probabilistic models
| Speaker: | Niklas Eiermann |
| Date: | 09.05.2023 |
Stochastic 3D microstructure modeling for electrodes in lithium-ion batteries
| Speaker: | Benedikt Prifling |
| Date: | 09.05.2023 |
Multivariate stochastic modeling by copulas at the example of multidimensional particle characteristics
| Speaker: | Selina Buck |
| Date: | 16.05.2023 |
The mineralogical composition of a particle system is characterised based on a total of six different characteristics describing size and shape of the particles, which are obtained through X-ray micro tomography measurements [1]. Since these six characteristics are highly correlated, it is difficult to estimate their joint probability distribution directly. Therefore, the marginal distributions of each characteristic are estimated separately, and their correlation structure is modelled by an Archimedean copula.
[1] O. Furat, T. Leißner, K. Bachmann, J. Gutzmer, U. Peuker and V. Schmidt, Stochastic modeling of multidimensional particle characteristics using parametric copulas. Microscopy and Microanalysis 25 (2019), 720-734
Stochastic modeling of curved fibers using R-vine copulas
| Speaker: | Eske Bockelmann |
| Date: | 16.05.2023 |
Nonwoven fiber-based material have important applications in various areas, such as fuel cell technology, filtration or hygiene products. In this work, a single-fiber model is proposed by describing a fiber as a sequence of bond and torsion angles. The whole fiber is then modelled by a k-th order Markov chain, where an R-vine copula is used to model the transition kernel of the Markov chain [2]. Simulating a set of fibers in this way generates a structure that exhibits similar properties to those observed in experimental data.
[2] M. Weber, A. Grießer, E. Glatt, A. Wiegmann and V. Schmidt, Modeling curved fibers by fitting R-vine copulas to their Frenet representations. Microscopy and Microanalysis (in print).
Generative flows for multivariate stochastic modeling
| Speaker: | Mathis Rost |
| Date: | 23.05.2023 |
Real-valued non-volume preserving (NVP) transformations are a class of functions used to construct a general unsupervised learning algorithm for generative probabilistic modeling. Unsupervised learning has the great advantage of not requiring a ground-truth, which is often produced by time consuming hand labelling. The model is trained on four natural image data sets and produces sharp and realistic images, that are qualitatively competitive with other generative probabilistic modeling algorithms [3].
[3] L. Dinh, J. Sohl-Dickstein, and S. Bengio. "Density estimation using real nvp." arXiv preprint arXiv:1605.08803 (2016).
The Boolean model: Basic properties and simulation algorithm
| Speaker: | Anina Dufter |
| Date: | 23.05.2023 |
The Boolean model is a powerful, but simple model in stochastic geometry. It is used as a baseline of many more complex models. The Boolean model is defined as union of independent and identically distributed random compact sets (called grains or particles), the random locations of which are given by a Poisson point process [4]. In this talk, basic properties of the Boolean model and a simulation algorithm will be presented.
[4] S.N. Chiu, D. Stoyan, W.S. Kendall, J. Mecke. Stochastic Geometry and its Applications, Chapter 3. J. Wiley & Sons (2013).
Using convolutional neural networks for stereological characterization of 3D hetero-aggregates
| Speaker: | Lukas Fuchs |
| Date: | 30.05.2023 |
Gaussian random fields for modeling three-phased microstructures
| Speaker: | Sebastian Acerbi |
| Date: | 30.05.2023 |
A Gaussian random field can be used for random sets by thresholding the field at a certain level. The points whose values exceed the threshold form a so called excursion set. By estimating the covariance function of the random field and the proper threshold, this set can then be used to model the solid phase of a given microstructure. By using two Gaussian random fields one can use this approach to also model three-phased structures, such as solid oxide fuel cells [5] or gas-diffusion electrodes [6].
[5] M. Neumann, B. Abdallah, L. Holzer, F. Willot and V. Schmidt, Stochastic 3D modeling of three-phase microstructures for predicting transport properties: a case study. Transport in Porous Media 128 (2019), 179-200
[6] M. Neumann, M. Osenberg, A. Hilger, D. Franzen, T. Turek, I. Manke, V. Schmidt, On a pluri-Gaussian model for three-phase microstructures, with applications to 3D image data of gas-diffusion electrodes. Computational Materials Science 156 (2019), 325-331
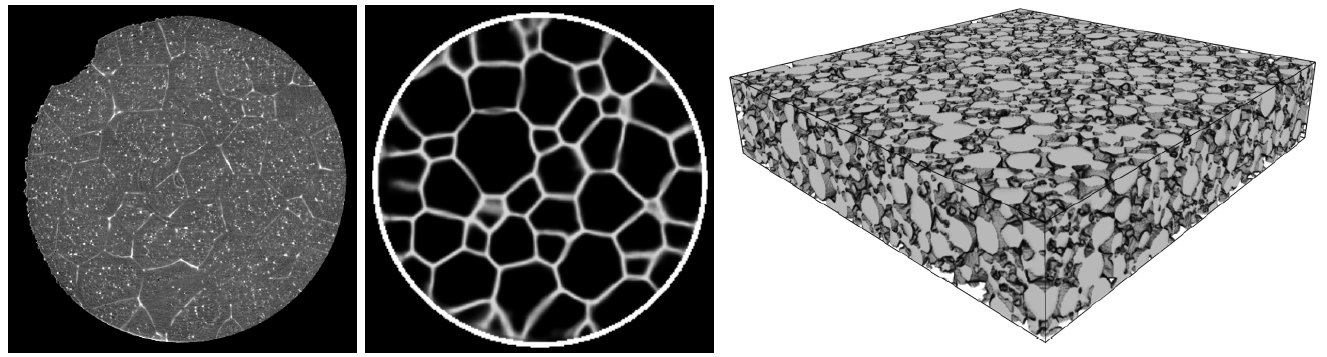
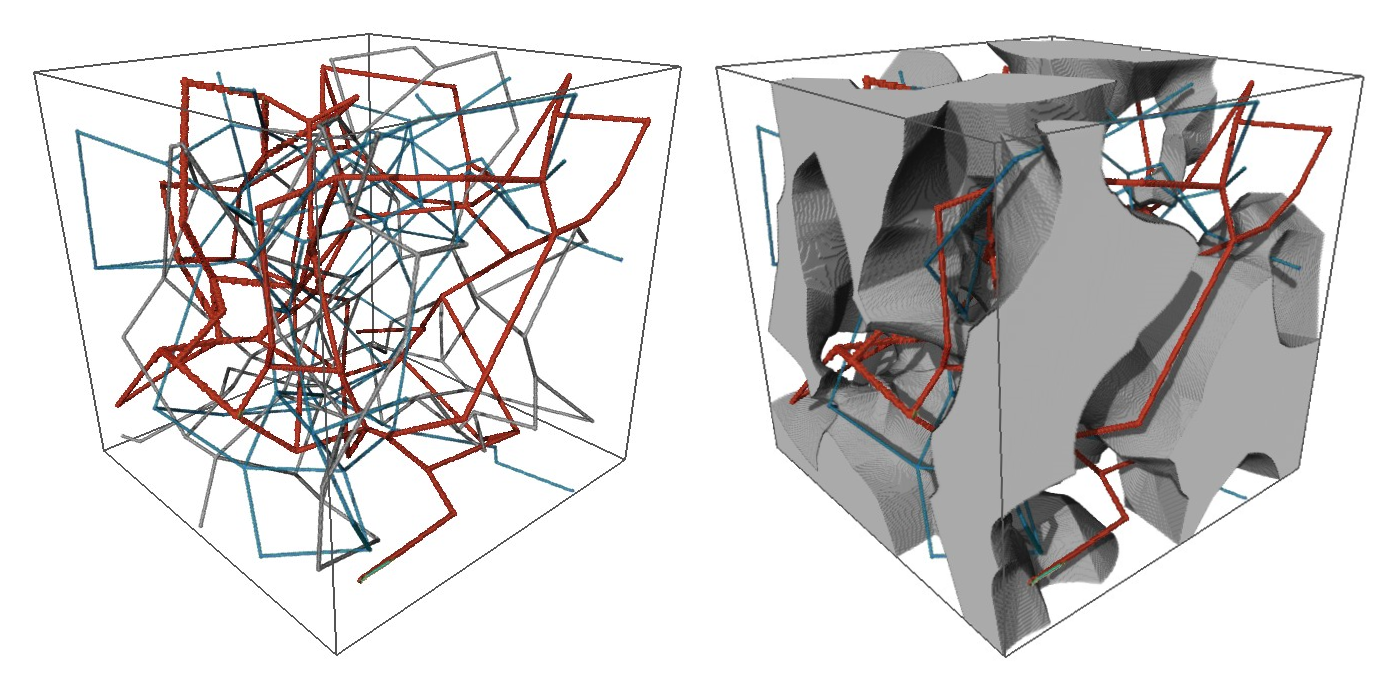
Graph based stochastic microstructure modeling: Generating digital twins of electrode materials
| Speaker: | Joana Dörr |
| Date: | 07.06.2023 |
By sampling a set of vertices from a random point process and connecting them in a deterministic way (according to the rule of beta-skeletons) we result in a random graph in the sense that the vertices are generated at random. This type of model can be used to model two- or three-phase materials, where connectivity properties of all phases can be nicely adjusted by parameters of the underlying graph. It has been used to model the microstructure of mesoporous silica [9] as well as solid oxide fuel cell electrodes [10].
[9] B. Prifling, M. Neumann, D. Hlushkou, C. Kübel, U. Tallarek and V. Schmidt, Generating digital twins of mesoporous silica by graph-based stochastic microstructure modeling. Computational Materials Science 187 (2021), 109934.
[10] M. Neumann, J. Stanek, O. Pecho, L. Holzer, V. Benes and V. Schmidt, Stochastic 3D modeling of complex three-phase microstructures in SOFC-electrodes with completely connected phases. Computational Materials Science 118 (2016), 353-364
Stochastic microstructure modeling, using Markov random fields
| Speaker: | Marita Dietz |
| Date: | 07.06.2023 |
Markov random fields (MRFs) are graph models, the vertices of which are random variables. The dependency structure of these random variables is tractable by the Markov property. By chosing a regular grid as the underlying graph, the realizations of the MRF can be considered to be images, i.e., MRFs can be used as random image models. Thus, have a broad range of applications ranging from image and texture synthesis, image compression and restoration, image segmentation and super-resolution to information retrieval [11]. Especially, using MRFs for image and texture synthesis makes them interesting as stochastic geometry models. In this talk basic properties of MRFs are given and an application for generating synthetic image data of polycrystalline materials is shown [12].
[11] L.Y. Wei, S. Lefebvre, V. Kwatra, G. Turk. State of the art in example-based texture synthesis. In Eurographics 2009, State of the Art Report, EG-STAR. Eurographics Association (2009), pp. 93-117.
[12] A. Kumar, L. Nguyen, M. DeGraef, V. Sundararaghavan, Markov random field approach for microstructure synthesis. Modelling and Simulation in Materials Science and Engineering (2016), 24(3), 035015.
Generative adversarial networks for the generation of multiphase microstructural data
| Speaker: | Argjend Fejzulahi |
| Date: | 13.06.2023 |
Generative adversial networks (GANs) which are usually models for unsupervised learning have, for example, various applications in texture and image synthesis [13]. After training with a given data set of images, these networks can generate new images which are statistically similar to those of the training data set. Therefore, GANs can be considered to be spatial stochastic models. For example, in [14] a GAN was trained with with 3D image data depicting the three-phased microstructure of lithium-ion battery cathodes and solid oxide fuell cell anodes. Then, similar to a stochastic geometry model, the trained network is able to generate virtual, but realistic 3D image data.
[13] I.J. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley, S. Ozair, A. Courville, Y. Bengio. Generative adversarial networks (2014). arXiv preprint arXiv:1406.2661.
[14] A. Gayon-Lombardo, L. Mosser, N.P. Brandon, S.J. Cooper. Pores for thought: generative adversarial networks for stochastic reconstruction of 3D multi-phase electrode microstructures with periodic boundaries. npj Computational Materials (2020), 6(1), 1-11.
Generating three-dimensional structures from a two-dimensional slice with generative adversarial network-based dimensionality expansion
| Speaker: | Rafael Schiafone |
| Date: | 13.06.2023 |
Generative adversarial networks (GANs) can be trained to generate 3D image data based on 3D training data. However, the acquisition 3D image data for model calibration is a time consuming and expensive task. While 2D image data naturally contains much less information, it is possible in some cases that a cross-sectional 2D slice carries enough information to statistically reconstruct the 3D sample. Therefore, a particular GAN-architecture is introduced that is able to generate 3D data based on a single representative 2D image [15].
[15] S. Kench, S.J. Cooper, Generating three-dimensional structures from a two-dimensional slice with generative adversarial network-based dimensionality expansion. Nat Mach Intell 3, 299–305 (2021).
Geometric data extraction and stochastic model-based simulation on different length scales
| Speaker: | Lukas Petrich |
| Date: | 29.06.2023 |
Adaptive blending of probabilistic precipitation forecasts with neural networks and the reintroduction of spatial information with the help of R-vine copulas
| Speaker: | Peter Schaumann |
| Date: | 29.06.2023 |
Copula-based modeling and simulation of systems of curved fibers by isolating intrinsic fiber properties and external effects
| Speaker: | Matthias Weber |
| Date: | 11.07.2023 |
Parameter estimation for graph-based stochastic microstructure models by means of convolutional neural networks
| Speaker: | Marten Ademmer |
| Date: | 11.07.2023 |
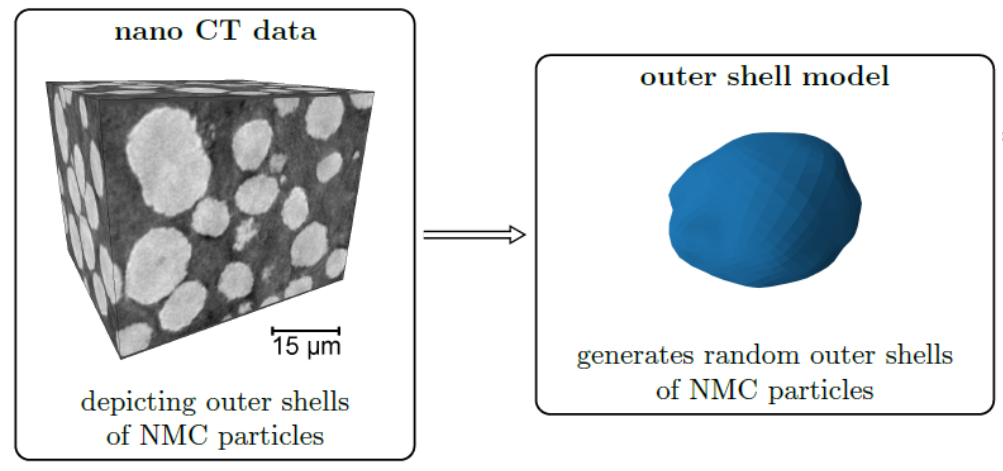
Generation of representative single Li-ion outer particle shells, using mixed Gaussian random fields on the unit sphere
| Speaker: | Markus Weidinger |
| Date: | 18.07.2023 |
Stochastic geometry models for the outer shell of individual particles are the basis for more complex models which consider the spatial positions of particles for the generation of virtual cathode microstructures. For modeling the shape of the outer shells of such particles often random fields on the unit sphere are used. In the Gaussian case the parameters of these models can be estimated using analytical formulas [7]. However, for more complex models (e.g, mixtures of Gaussian random fields) a direct estimation of model parameters is difficult. In this case machine learning libraries can be utilized for a fast optimization of model parameters [8].
[7] J. Feinauer, T. Brereton, A. Spettl, M. Weber, I. Manke and V. Schmidt, Stochastic 3D modeling of the microstructure of lithium-ion battery anodes via Gaussian random fields on the sphere. Computational Materials Science 109 (2015), 137-146.
[8] O. Furat, L. Petrich, D. Finegan, D. Diercks, F. Usseglio-Viretta, K. Smith and V. Schmidt, Artificial generation of representative single Li-ion electrode particle architectures from microscopy data. npj Computational Materials 7 (2021), 105.
Prediction of mineralogical particle composition for the evaluation of separation processes using CT data and R-vine copulas
| Speaker: | Sabrina Weber |
| Date: | 18.07.2023 |